[Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 순환 (Recursion) 의 응용 : 미로찾기

 

미로 찾기

 

그리드의 크기 : N x N (N-1, N-1)

현재 위치에서 출구까지 가는 경로가 있으려면

1) 현재 위치가 출구이거나

2) 이웃한 셀들 중 하나에서 현재 위치를 다시 지나지 않고 출구까지 가는 경로가 있거나

 

 

STEP 1. 현재 위치에서 출구까지 가는 경로가 있는지 없는지 확인하는 코드
                즉, 이 알고리즘의 핵심 부분을 설명하는 Decisioin Problem을 작성한다.

 

if (x,y) is the exit

   return true;

-> 현재 위치가 출구이면 경로가 있다.

 

for each neighbouring cell (x',y') of (x,y) do

   if (x',y') is on the pathway

      if findPath(x',y')

         return true;

-> 현재 위치와 근접한 각각의 셀들 중에서 벽을 제외한 셀들에 대해 출구까지 가는 경로가 있는지 recursive하게 확인한다.

     = 현재 위치와 근접한 셀들 중 벽이 아닌 길이라면 출구까지의 경로를 반복적으로 탐색한다.

 

return false;

-> 위 코드에서 true값이 반환되지 않고 아래 코드로 내려왔다 = 현재 위치와 인접한 각각의 셀들 중에서 출구까지 가는 경로가 없다.

 

 

 

 

 

STEP 2. 해당 알고리즘이 무한루프에 빠지지 않는지 검사한다.

 

 

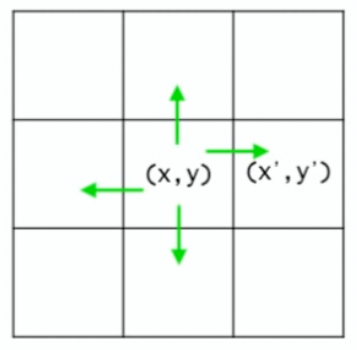
이 경우에는 findPath(x,y)가 인접 셀인 (x',y')를 호출했을 때 findPath(x',y')

옮겨온 셀 (x',y') 입장에서는 (x,y)가 자신에게 인접한 셀이 되어 findPath(x,y)를 호출해

findPath(x,y)는 findPath(x',y')를 계속 호출하고, findPath(x',y')는 findPath(x,y)를 계속 호출하는 무한 루프에 빠진다.

 

 

 

 

 

이런 일은 어떻게 방지할 수 있을까?

이미 가본 위치와 가보지 않은 위치를 구별해서 가보지 않은 셀들을 대상으로 경로를 탐색한다.

예를 들어, 이미 방문한 셀에는 visited = 1이라고 표시를 하고

이웃한 셀들 중 아직 방문하지 않은 셀 (visited = 0)만 호출할 수 있도록 하면 무한루프 문제를 막을 수 있다는 것이다.

 

 

현재 위치 (x,y)에서 인접한 셀인 (x',y')에 대한 탐색을 시작할 때 먼저 "이 셀은 방문했다!!"고 visitied=1처럼 표시해두고 다음 단계로 넘어간다. 그 후, 다른 셀에서 (x',y')를 탐색하려고 할 경우, visitied 값을 확인하여 방문했다고 표시되어 있는 셀이라면 탐색을 생략해서 무한루프에 빠지지 않게 한다.

 

 

따라서, STEP 1 코드와 합치게 되면

인접한 셀들 중, 1) 벽이 아닌 통로이고 2) 방문한 적이 없는 셀에 대해서만 출구까지의 경로를 찾으면 된다.

 

 

혹은 반대로,

아예 함수의 첫 부분에서 1) 통로가 아닌 벽이고 2) 방문한 적이 있는 셀 이라면 경로를 탐색할 조건에 부합하지 않다고 판단하여 false를 반환해버리게 구현할 수도 있다.

=> 위 코드가 최종적인 sudo code로 이 방식으로 구현할 예정

 

 

 

 

 

STEP 3. 구현

visited = PATH_COLOUR(방문했는데 출구까지 가는 경로인 셀), BLOCKED_COLOUR(방문했지만 출구까지 가는 경로가 아닌 셀)

셀의 좌표가 그리드에서 벗어난 경우 false, 해당 셀이 0이 아닌 경우(방문한 적이 있거나 벽인 경우) false, 도착 지점을 찾은 경우 true 리턴

북->동->남->서 순서로 우선순위를 두고 탐색. 얼마든지 변경가능. 주변 모든 셀에서 경로를 찾지 못했다면 해당 셀 false

 

 

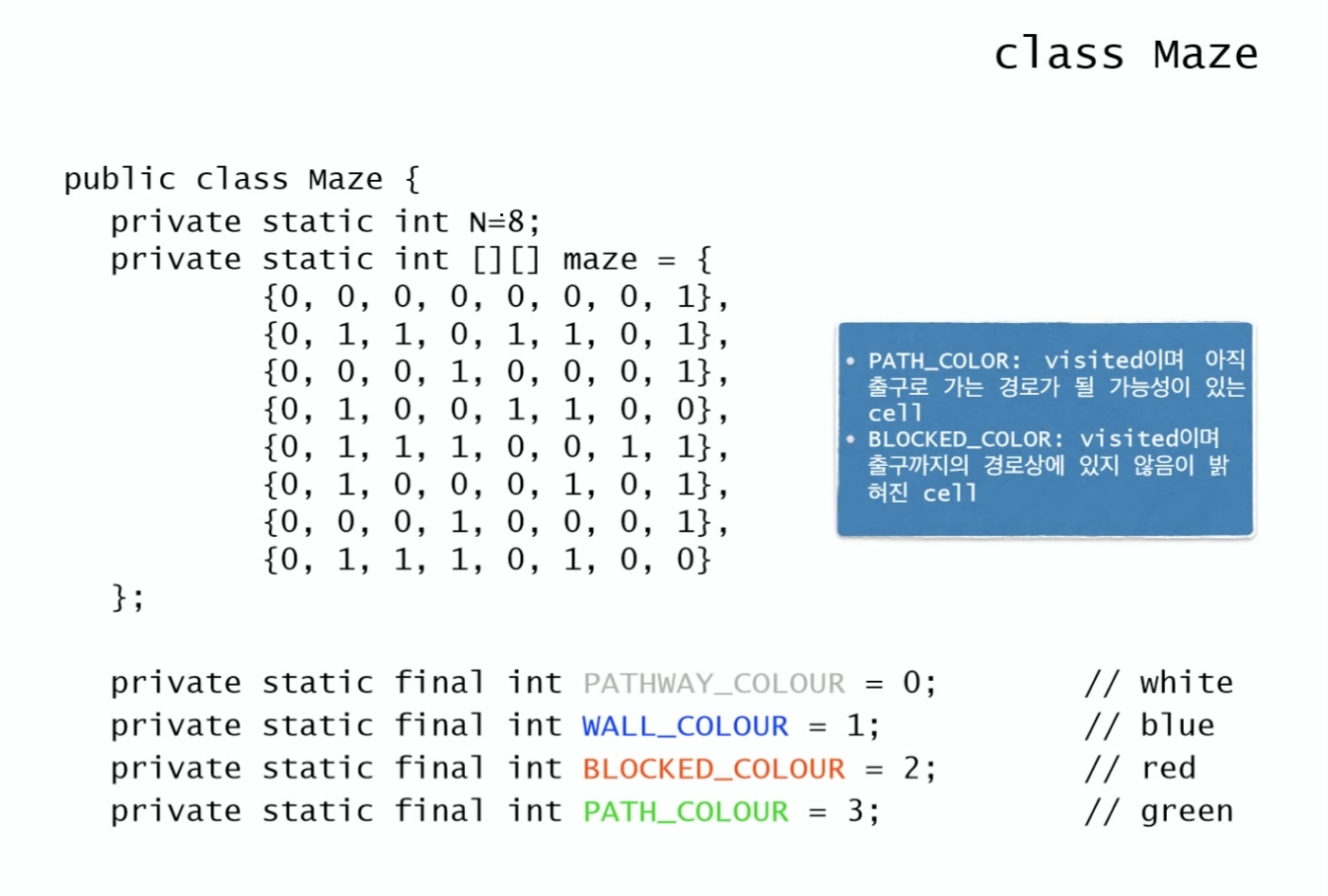
미로 탐색 경로

 

 

 

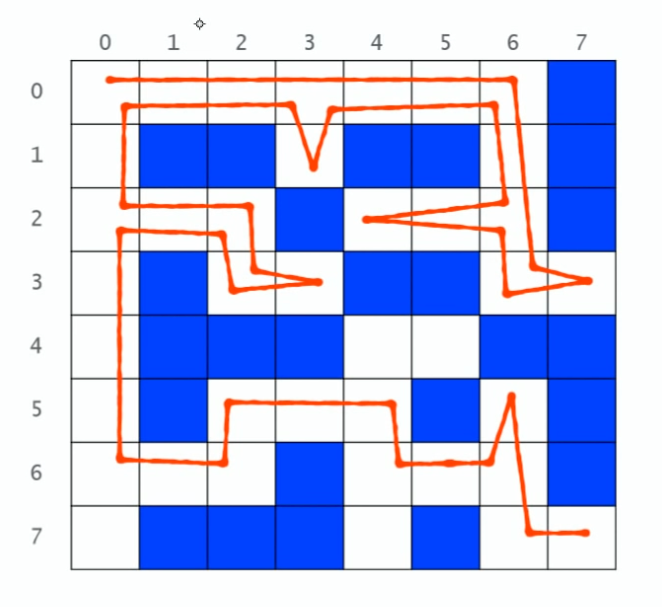
코드

import java.util.Scanner;

public class example {
    private static int N=8;
    private static int[][] maze = {
            {0,0,0,0,0,0,0,1},
            {0,1,1,0,1,1,0,1},
            {0,0,0,1,0,0,0,1},
            {0,1,0,0,1,1,0,0},
            {0,1,1,1,0,0,1,1},
            {0,1,0,0,0,1,0,1},
            {0,0,0,1,0,0,0,1},
            {0,1,1,1,0,1,0,0}
    };

    private static final int PATHWAY_COLOUR = 0;
    private static final int WALL_COLOUR = 1;
    private static final int BLOCKED_COLOUR = 2; // 방문해서 PATH_COLOUR이었다가 경로가 아니라고 판단된 셀
    private static final int PATH_COLOUR = 3; // 방문했고 아직 꽝인지 출구까지 경로인지 모르는 셀

    public static boolean findMazePath(int x, int y) {
        if (x<0 || y<0 || x>=N || y>=N) return false; // 그리드 벗어나는 위치라면 false
        else if (maze[x][y] != PATHWAY_COLOUR) return false; // 방문했던 셀이라면 false
        else if(x==N-1 && y==N-1) { // 도착 위치(최종 경로)를 찾았다면 true
            maze[x][y]=PATH_COLOUR;
            return true;
        }
        else { // 인접 셀을 통해 경로 찾기
            maze[x][y] = PATH_COLOUR; // 방문했지만 아직 꽝인지 아닌지 몰라! 그렇지만 재탐색은 안돼!
            if(findMazePath(x,y+1) || findMazePath(x+1, y) || findMazePath(x,y-1) || findMazePath(x-1,y))
                return true; // 인접한 셀들 중 경로가 있다면 그 방향으로 계속 탐색을 반복해
            maze[x][y] = BLOCKED_COLOUR; // 방문했지만 꽝이야 그쪽엔 길 없어
            return false; // 그 경로로는 탐색 그만해 -> 다른 경로로 탐색해보자
        }
    }

    public static void printMaze() {
        for (int i = 0; i < maze.length; i++) {
            for (int j = 0; j < maze[i].length; j++) {
                System.out.print(maze[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        printMaze();
        findMazePath(0,0);
        System.out.println();
        printMaze();
    }
}

 

 

결과

공백 위에는 초기 미로를, 공백 아래는 경로를 찾은 미로를 나타낸다

근접 셀들을 방문할 때 PATH_COLOUR=3로 "방문한 셀이야"라고 표시해 놓고 길이 없으면 BLOCKED-COLOUR=2로 변경한다.

따라서 2라고 표시된 곳들은 이미 방문했지만 (N-1, N-1)까지 경로가 없는 셀들이다. (말그대로 "막힌 길")

3으로 표시된 셀들을 이어나가보면 미로 탐색 경로 사진에서 찾았던 경로와 일치하는 출구까지의 경로를 찾을 수 있다.