합병 정렬 (merge sort)
지난 시간에 버블 정렬, 삽입 정렬, 선택 정렬에 대해 배웠다.
https://rookie-programmer.tistory.com/51
[Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 기본적인 정렬 알고리즘
정렬 알고리즘 Selection sort, Bubble sort, Insertion sort * 버블 정렬, 삽입 정렬, 선택 정렬 : 구현이 단순하지만 속도가 느림 * 퀵 정렬, 합병(병합) 정렬, 힙 정렬 : 구현이 복잡하지만 속도가 빠름 * Radix
rookie-programmer.tistory.com
이번 시간부터는 그것들보다 실행 속도는 빠르지만 구현이 어려운 합병 정렬, 퀵 정렬, 힙 정렬에 대해 배운다.
합병 정렬, 퀵 정렬은 "분할정복법(Divide and Conquer)"을 이용하여 쉽게 정렬할 수 있다.
"분할정복법(Divide and Conquer)"이란?

해결하고자 하는 문제를 작은 크기의 "동일한 문제들"로 쪼개 작은 문제들을 반복적으로 해결해나가는 것이다.

ALGORITHMS 문자 배열을 정렬하는 것을 분할정복법으로 생각한다면
절반으로 나눠서 나뉜 2개의 배열 덩이로 나눠 (작은 크기의 동일한 문제로 divide)
각각의 배열을 먼저 정렬한 후 (recursively sort)
2개의 배열을 합치면서 정렬해 최종 해를 구한다. (merge)

작은 크기의 동일한 문제로 나누는 것을 반복하다 보면 위의 그림처럼 숫자가 1개일 때까지 나눠진 후
합치는 과정에서 정렬하는 동작을 반복해 최종 해를 구한다.
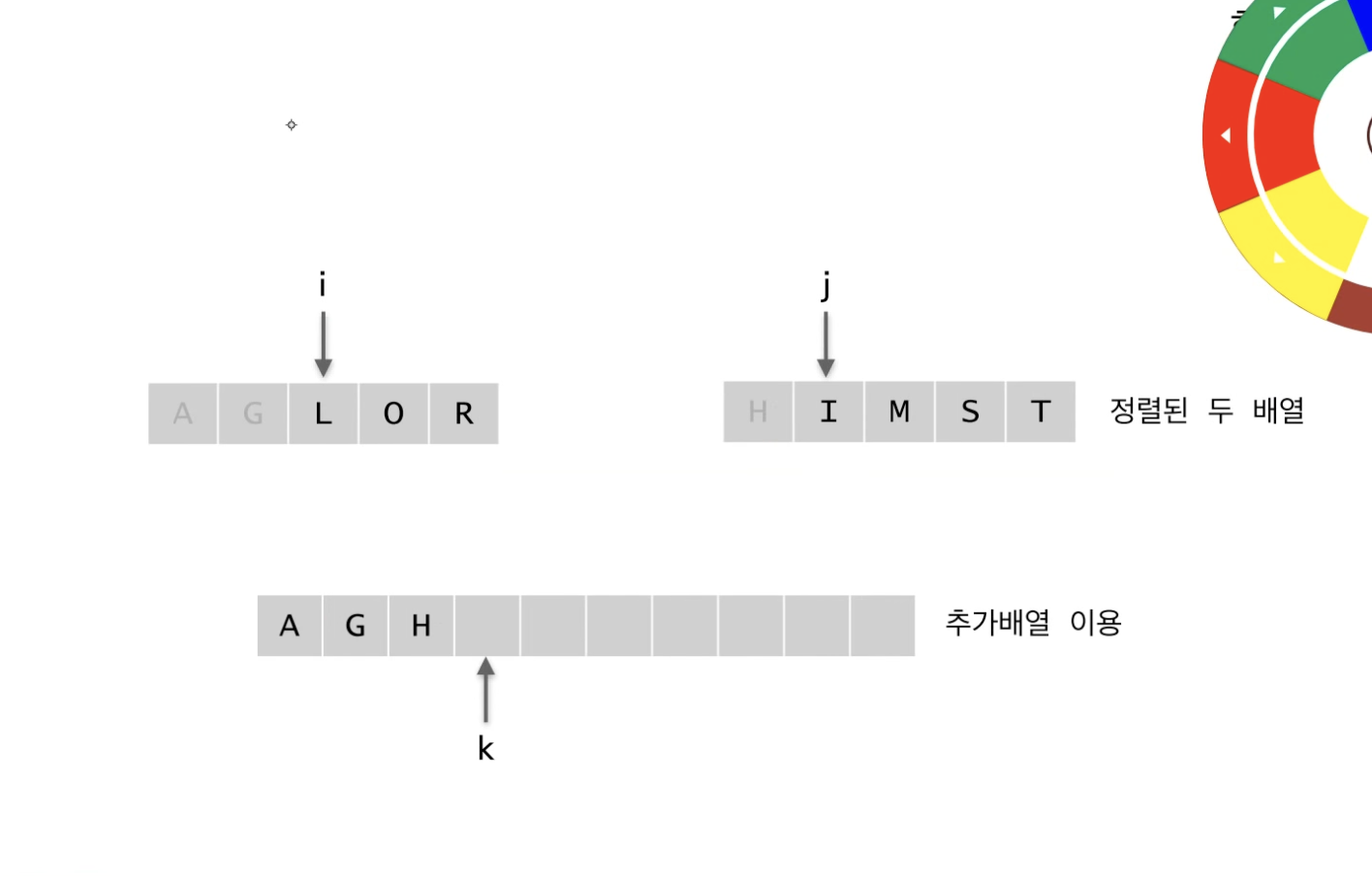
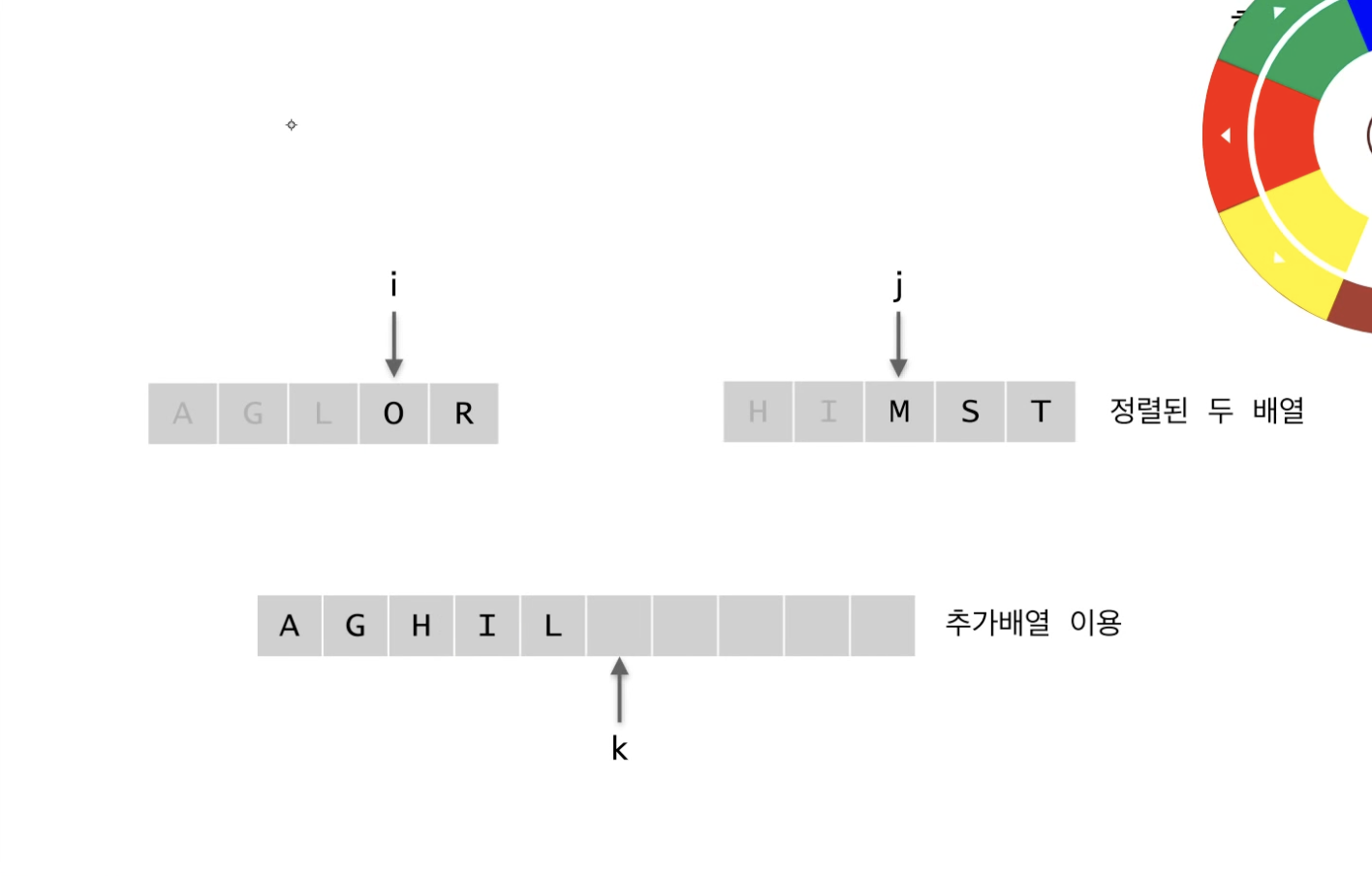
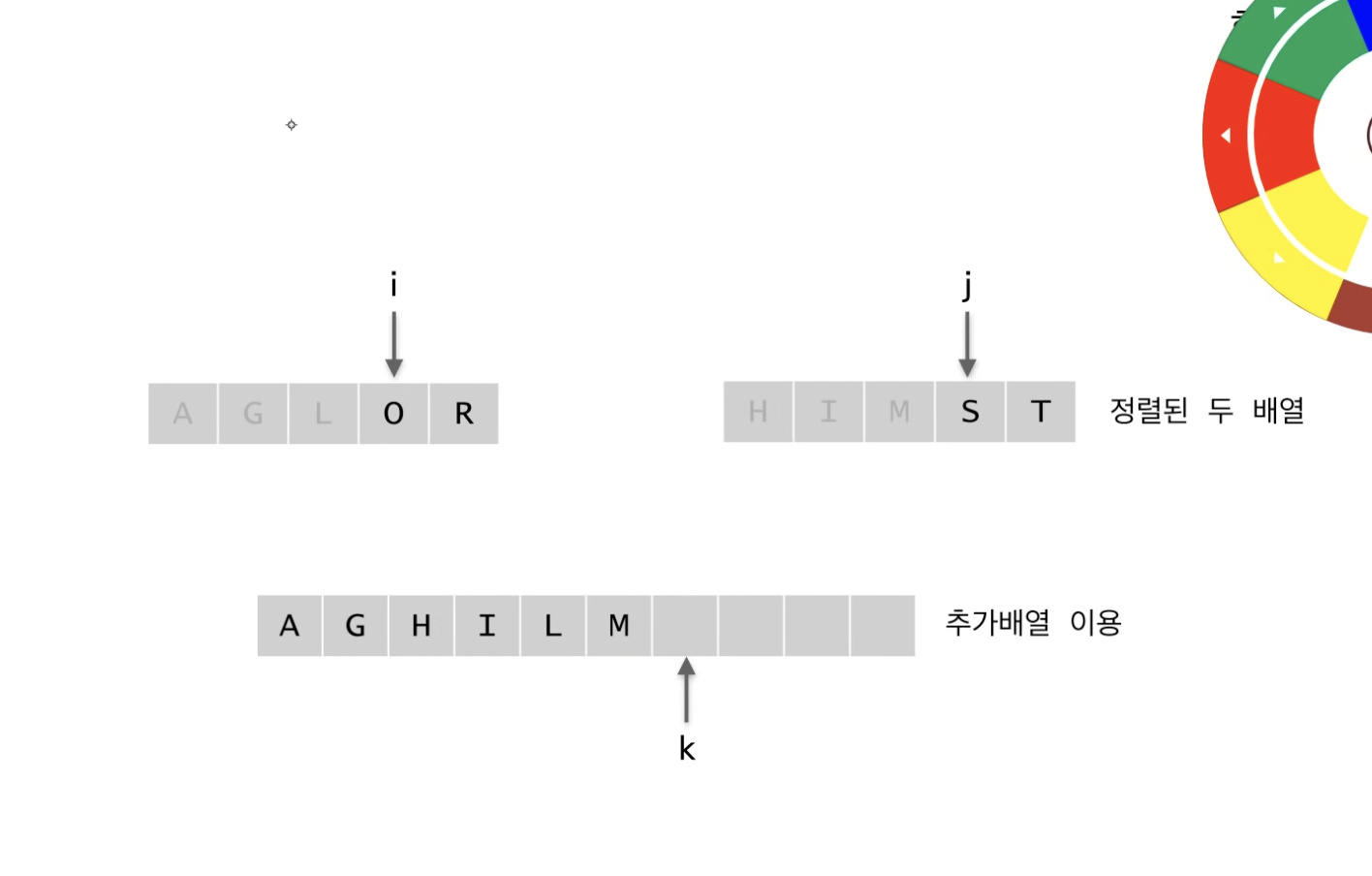
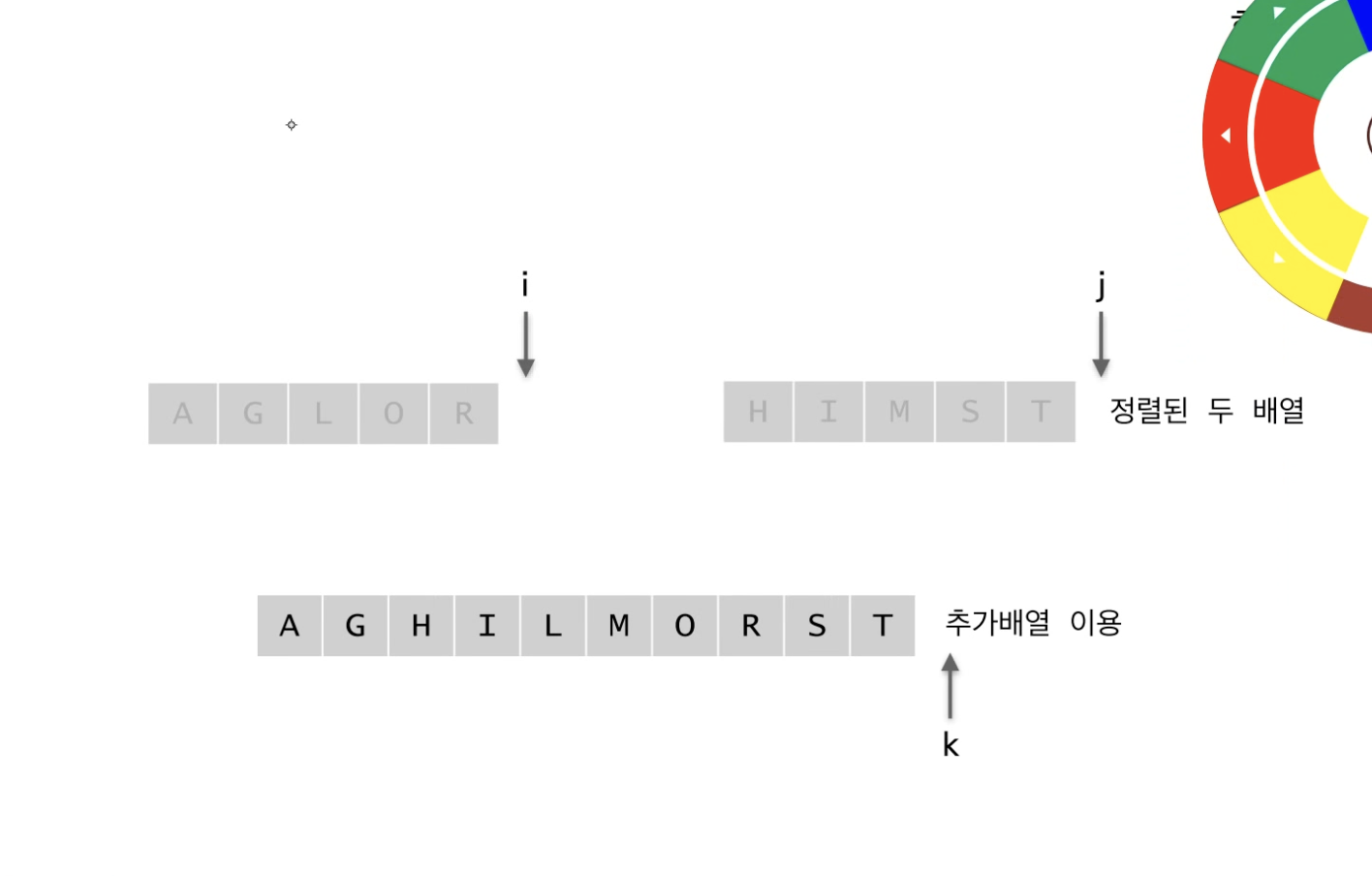
merge 하는 과정 ⭐⭐⭐⭐⭐

합쳐지는 대상이 되는 두 개의 배열은 정렬이 되어 있기 때문에
각 배열의 맨 왼쪽 값부터 차례대로 비교해서 작은 값을 추가배열에 넣어주는 과정을 반복하면 된다.
한 쪽 배열의 값이 모두 추가배열에 들어간다면, 다른 쪽 배열의 값은 비교없이 모두 추가배열에 넣어주면 된다.





알고리즘

mergeSort()로 배열을 2개로 나누는 작업과 배열을 합치며 정렬하는 작업을 반복한다.
이것을 코드로 구현해보자.

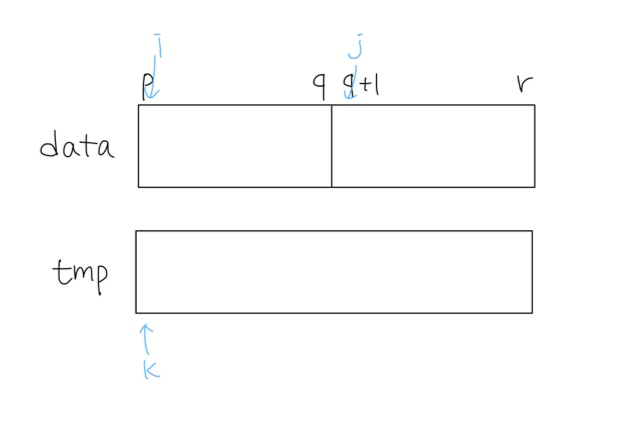
data에 있는 배열이 절반 지점인 q를 기준으로 p~q, q+1~r 두 부분으로 나뉜다.
두 부분의 값을 비교하여 작은 값을 갖는 숫자를 tmp로 옮겨준다.
한 쪽의 값이 먼저 전부 옮겨진다면 나머지 한 쪽의 값은 비교없이 차례대로 다 옮겨준다. (이미 정렬되어 있는 상태이기 때문)
마지막 for문을 통해 두 부분을 합친 결과물을 기존 배열에 업데이트 해준다.
* 합병(병합) 정렬의 시간복잡도 : O(n logn)
최악의 경우 = 평균의 경우 = 최선의 경우

n번 비교 * 트리의 높이 log n = n log n
* 합병 정렬 자바 코드 ( merge sort java code )
import java.util.Arrays;
public class sort {
public static void mergeSort(int[] a, int p, int r) {
if(p<r) {
int q = (p+r)/2;
mergeSort(a, p, q);
mergeSort(a, q+1, r);
merge(a, p, q, r);
System.out.println(Arrays.toString(a));
}
}
public static void merge(int[] a, int p, int q, int r) {
int i=p, j=q+1, k=p;
int[] tmp = new int[a.length];
while(i<=q && j<=r) {
if(a[i] <= a[j])
tmp[k++] = a[i++];
else
tmp[k++] = a[j++];
}
while(i<=q) tmp[k++] = a[i++];
while(j<=r) tmp[k++] = a[j++];
for (int l = p; l <= r; l++) {
a[l] = tmp[l];
}
}
public static void main(String[] args) {
int[] a = new int[]{4, 9, 2, 6, 8, 5, 7, 1, 3};
mergeSort(a, 0, a.length-1);
}
}결과

'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 빠른 정렬 (quick sort) (0) | 2022.12.15 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #03-03 3. 최대 매출 (0) | 2022.12.15 |
| [Inflearn] 자바 알고리즘 문제풀이 #03-02 2. 공통원소 구하기 (0) | 2022.12.14 |
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 기본적인 정렬 알고리즘 (0) | 2022.12.13 |
| [Inflearn] 자바 알고리즘 문제풀이 #03-01 1. 두 배열 합치기 (0) | 2022.12.13 |



