문제
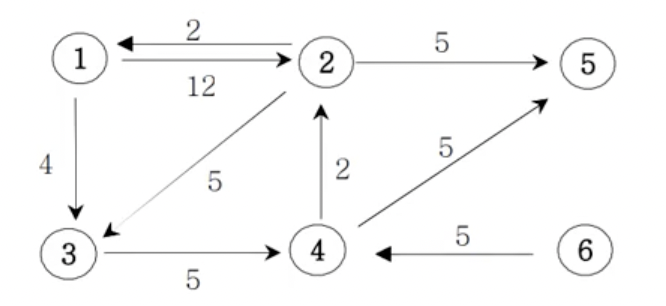
아래의 가중치 방향그래프에서 1번 정점에서 모든 정점으로의 최소 거리비용을 출력하는 프로그램을 착성하세요.
(경로가 없으면 Impossible을 출력한다)
입력
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보와 거리비용이 주어진다.
출력
1번 정점에서 각 정점으로 가는 최소비용을 2번 정점부터 차례대로 출력하세요.
예시 입력 1
6 9
1 2 12 // 1번 정점에서 2번 정점으로 가는데 12 비용이 든다
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
예시 출력 1
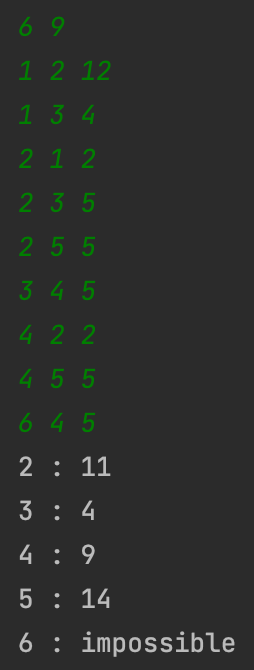
2 : 11
3 : 4
4 : 9
5 : 14
6 : impossible
코드
import java.util.*;
class Edge implements Comparable<Edge>{
public int vex;
public int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main9_5 {
static int n, m;
static ArrayList<ArrayList<Edge>> graph;
static int[] dis;
public void solution(int v){
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(v, 0));
dis[v]=0;
while(!pQ.isEmpty()){
Edge tmp=pQ.poll();
int now=tmp.vex;
int nowCost=tmp.cost;
if(nowCost>dis[now]) continue; //이미 뻗어져 나간 값보다 꺼낸 객체의 cost가 크다면 생략
for(Edge ob : graph.get(now)){
if(dis[ob.vex]>nowCost+ob.cost){
dis[ob.vex]=nowCost+ob.cost;
pQ.offer(new Edge(ob.vex, nowCost+ob.cost));
}
}
}
}
public static void main(String[] args){
Main9_5 T = new Main9_5();
Scanner kb = new Scanner(System.in);
n=kb.nextInt();
m=kb.nextInt();
graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
dis=new int[n+1];
Arrays.fill(dis, Integer.MAX_VALUE);
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
graph.get(a).add(new Edge(b, c));
}
T.solution(1);
for(int i=2; i<=n; i++){
if(dis[i]!=Integer.MAX_VALUE) System.out.println(i+" : "+dis[i]);
else System.out.println(i+" : impossible");
}
}
}
graph는 Edge를 담을 수 있는 ArrayList들을 담는 ArrayList (조금 복잡하다ㅎㅎ)
graph를 위의 그림처럼 만들어두고 사용하려면 아래 코드가 필요하다.
graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
graph를 만들었다면 정점-비용 정보를 입력받을 때 아래와 같이 넣어주면 된다.
graph.get(a).add(new Edge(b, c));
1) 다익스트라 - O(n^2) 시간복잡도일 경우
1번 정점부터 N번 정점까지 반복 --> n
각 반복에서 길이N 배열에서 최소값 찾기 --> n
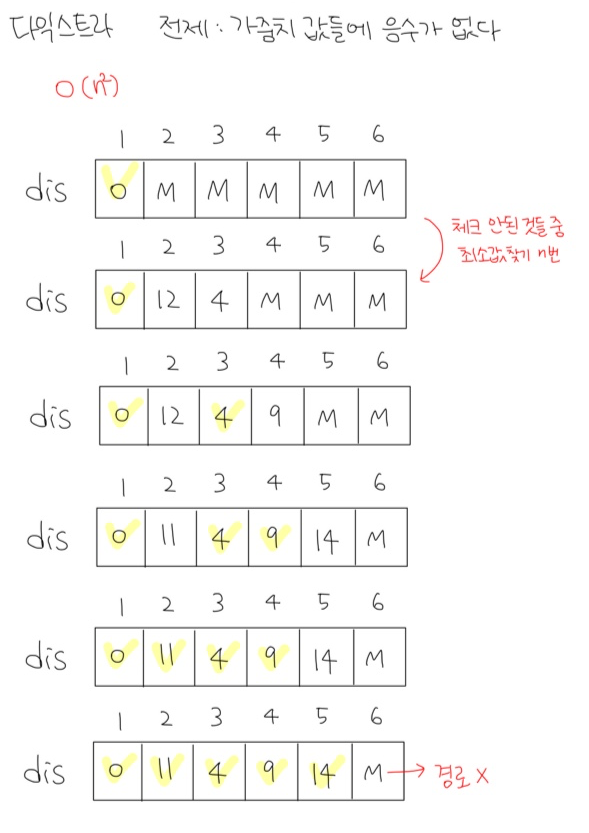
dis 배열에서 시작점은 0, 나머지 정점은 MAX 값으로 설정
시작점인 1번 정점부터 연결되어 있는 간선의 비용을 확인해
비용의 값이 이전 경로의 비용보다 작다면 업데이트, 아니라면 패스
다음 정점을 선택하는 기준은 가보지 않음 + 최소 비용 값을 가짐
N번 반복해서 업데이트, M값을 가지는 것은 경로가 없다는 것
2) 다익스트라 - O(n lon n) 시간복잡도일 경우
1번 정점부터 N번 정점까지 반복 --> n
각 반복에서 우선순위 큐에서 최소값 찾기 --> log n
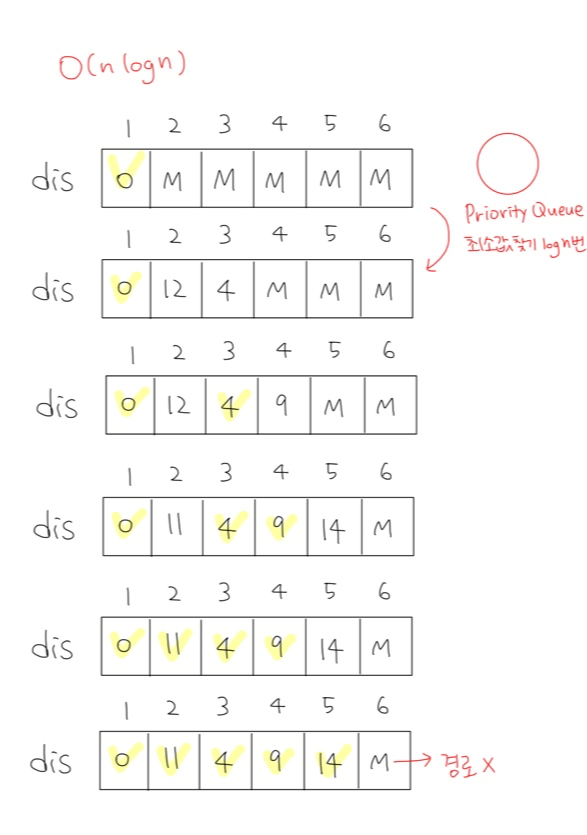
1번 방식에서 최소값을 찾는 방법만 다르다.
구현 코드는 2번 방식을 택했다.
결과
'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 자바 알고리즘 문제풀이 #09-07 7. 원더랜드(최소 스패닝 트리 - 크루스칼 : Union&Find 이용) (0) | 2023.08.07 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #09-06 6. 친구인가? (Disjoint-Set : Union&Find) (0) | 2023.07.31 |
| [Inflearn] 자바 알고리즘 문제풀이 #09-04 4. 최대 수입 스케쥴(PriorityQueue 응용문제) (0) | 2023.07.17 |
| [Inflearn] 자바 알고리즘 문제풀이 #09-03 3. 결혼식(Greedy Algorithm) (0) | 2023.05.19 |
| [Inflearn] 자바 알고리즘 문제풀이 #09-02 2. 회의실 배정(Greedy Algorithm) (0) | 2023.05.12 |



