[Inflearn] 자바 알고리즘 문제풀이 #09-06 6. 친구인가? (Disjoint-Set : Union&Find)

문제

설명

오늘은 새 학기 새로운 반에서 처음 시작하는 날이다. 현수네 반 학생은 N명이다. 현수는 각 학생들의 친구관계를 알고 싶다.

모든 학생은 1부터 N까지 번호가 부여되어 있고, 현수에게는 각각 두 명의 학생은 친구 관계가 번호로 표현된 숫자쌍이 주어진다.

만약 (1, 2), (2, 3), (3, 4)의 숫자쌍이 주어지면 1번 학생과 2번 학생이 친구이고, 2번 학생과 3번 학생이 친구, 3번 학생과 4번 학생이 친구이다.

그리고 1번 학생과 4번 학생은 2번과 3번을 통해서 친구관계가 된다.

학생의 친구관계를 나타내는 숫자쌍이 주어지면 특정 두 명이 친구인지를 판별하는 프로그램을 작성하세요.

두 학생이 친구이면 “YES"이고, 아니면 ”NO"를 출력한다.

 

입력 

첫 번째 줄에 반 학생수인 자연수 N(1<=N<=1,000)과 숫자쌍의 개수인 M(1<=M<=3,000)이 주어지고,

다음 M개의 줄에 걸쳐 숫자쌍이 주어진다.

마지막 줄에는 두 학생이 친구인지 확인하는 숫자쌍이 주어진다.

 

출력 

첫 번째 줄에 “YES"또는 "NO"를 출력한다.

 

예시 입력 1 

9 7
1 2
2 3
3 4
1 5
6 7
7 8
8 9
3 8

예시 출력 1

NO

 

 

 

선생님 풀이

import java.util.Scanner;

public class Main9_6 {
    static int[] unf;
    public static int Find(int v) {
        //v와 연결된 친구 중 가장 마지막 친구를 찾으면서 그 값을 unf[v]에 업데이트
        if(v==unf[v]) return v;
        else return unf[v] = Find(unf[v]);
    }
    public static void Union(int a, int b) {
        int fa = Find(a);
        int fb = Find(b);
        if(fa!=fb) unf[fa] = fb; //a-b 친구 연결
    }

    public static void main(String[] args){
        Main9_6 T = new Main9_6();
        Scanner kb = new Scanner(System.in);
        int n=kb.nextInt();
        int m=kb.nextInt();
        unf=new int[n+1];
        for(int i=1; i<=n; i++) unf[i]=i;
        for(int i=1; i<=m; i++){
            int a=kb.nextInt();
            int b=kb.nextInt();
            T.Union(a, b);
        }
        int a=kb.nextInt();
        int b=kb.nextInt();
        int fa=T.Find(a);
        int fb=T.Find(b);
        if(fa==fb) System.out.println("YES");
        else System.out.println("NO");
    }
}

Find 함수

학생V의 “집합 번호”를 리턴

인덱스 번호와 집합 번호가 같다면 인덱스 번호 리턴

다르다면 연결된 마지막 꼬리 번호를 리턴 ⭐️⭐️

 

Find 함수에서 else return Find(unf[v])일 경우

1-2-3-4 연결된 상태에서 1-5가 입력되면

1-2-3-4-5처럼 5가 꼬리의 끝에 연결되는데

1번 관련 작업 실행될 때마다 2->3->4 호출 발생해 비효율

아래의 그래프 그림에서 1-2-3-4-5 일렬로 연결된 그래프 모양을 갖게 된다.

 

 

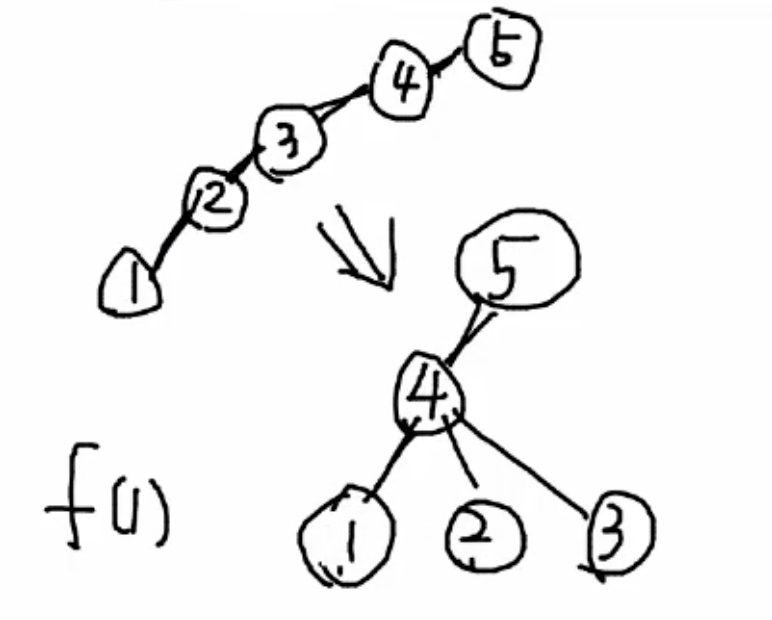
Else return unf[v] = Find(unf[v])일 경우 —> “경로 압축” —> 배열에 꼬리 끝 값 업데이트 해두고 한 번에 찾겠다

1-2-3-4 연결된 상태에서 1-5가 입력되면 Union(1, 5)실행

fa값을 찾는 과정에서 Find(1) 실행 -->

V!=unf[v]이기 때문에 Find(2) -> Find(3) -> Find(4) 순차 호출하면서 1-2-3-4 연결된 그래프 모양을 만든다.

 

 

여기서 (1, 5)입력이 들어왔을 때 경로 압축이 발생한다.

Find(v)함수의 의미를 다시 살펴보면, 연결된 마지막 꼬리 번호를 리턴한다는 뜻이다

 

최근에 호출된 순서대로 Find(4) -> Find(3) -> Find(2) -> Find(1) 내려오면서 unf[v]값을 갱신한다.

 

 

 

 

 

 

Find(4) - V==unf[v]이기 때문에 4반환

Find(3) - unf[3] = 4

Find(2) - unf[2] = 4

Find(1) - unf[1] = 4

1, 2, 3 모두 꼬리 끝 번호는 4이므로 unf[1] unf[2] unf[3] 값이 모두 4로 변경된다.

이는 위의 그래프 그림에서 아래에 위치한 그래프 모양을 갖게 변화하며

1->5가 들어왔을 때 1-2-3-4-5 모두 호출하는 것이 아니라 1->4->5를 호출해 효율적인 접근이 가능하게 만든다.

 

 

 

결과