n queens problem
문제
n queens problem이란 무엇인가?
n*n 체스판에서 어떠한 두 말도 동일한 행이나 열, 동일한 대각선 상에 오지 않도록 n개의 말을 놓을 수 있느냐의 문제

알고리즘
하나의 말을 첫 행의 아무 위치에 일단 놓은 후, 나머지 행에 다른 말들을 모두 놓을 수 있는지 확인한다.
확인하는 과정에서 back tracking 방법이 사용된다.
back tracking이란?
말을 두었다가 문제를 해결하지 못할 경우 해당 위치에 말을 둔 결정을 번복하고 다른 위치에서 문제를 해결할 방법을 찾는 것이다.
쉽게 말하면 "무르기!"다.
(사람이 노가다로 문제를 풀려고 하는 방식과 원리가 같으니 4x4체스판으로 한 번 해보면 더 알기 쉬울 것 같다.)
SW적 용어로는 그래프의 깊이우선 탐색 기법이라고 한다.

노트를 순차적으로 탐색하다가 불가능한(infeasible) 노드를 만난다면 이전으로 돌아가서 해당 노드를 다른 위치에 다시 놓는 방법이다.
위 그림처럼 1번 말을 1, 1 위치에 놓으면 2, 1과 2, 2에는 다른 말을 놓을 수 없으니 더 이상 그 아래로 경로를 탐색하지 않고 그 결정을 물러 1, 1 노드로 돌아간 후, 1번 말과 충돌이 일어나지 않는 위치인 2, 3과 2, 4에 놓아 경로를 찾아보는 것이다.

위 문제는 상태공간트리(찾는 해를 포함하는 트리)로 풀어내면 되는데
1번 말을 1, 1 위치에 놓고, 나머지 말들을 하나씩 모든 열에 놓으면서 해가 생기는지 생기지 않는지 판단하여 해를 구하는 방법이다.
1번 말을 1, 1 위치에 놓았지만 나머지 말들을 각각 2행, 3행, 4행에 다 놓지 못했다면 문제를 풀지 못한 것으로 간주하고 1번 말을 놓았던 것을 무르고, 1번 말을 다시 1, 2 위치에 놓고 나머지 말들을 고려한다.
계속 문제를 풀지 못했다면 1번 말을 1, 4 위치(1행의 맨 오른쪽 위치)에 놓을 때까지 반복한다.
그렇지만 상태공간트리의 모든 말들을 모든 노드에 놓고 N^n의 모든 경우의 수를 따져봐야 하는 것은 아니다.
1번 말을 1, 1위치에 놓았다면 2번 말은 1번 말과 충돌이 일어나는 2, 1과 2, 2 위치에는 놓을 수 없으니 2, 3과 2, 4에 놓는 경우만 고려해주면 된다.
( non-promising = infeasible한 해 = 이전 말들과 충돌하는 위치에 있는 해 = 더이상 살펴보지 않아도 답이 없는 해 = 꽝인 노드)
sudo code

꽝인 노드라면 무르고 이전 노드로 돌아가기,
경로를 찾았다면 탐색 끝내기,
둘 다 아니라면 자식 노드들을 반복적으로 탐색한다.

이때 매개변수 level로 현재 노드의 행을 표현하고, cols 배열로 열을 표현하자.
1번 말은 level 1에, 2번 말은 level 2에 있고 cols[i] = j는 i번 말이 (i행, j열)에 놓였음을 의미한다.
여기서는 level값이 i가 되는 것이고
cols[1] : 1번 말이 놓인 열 번호, cols[2] : 2번 말이 놓인 열 번호로 해석하면 된다.

return type은 boolean으로 설정해주어 답이 아닐 경우 false, 답일 경우 true를 반환해 탐색을 하게 해준다.
if -> promising 함수를 만들어 해당 노드가 답이 있는 노드인지 판별해 답이 없다면 해당 노드의 탐색을 종료한다.
else if -> level이 N과 같다는 뜻은 N개의 말이 다 놓였다는 뜻이다. (그래야 N개의 level이 생기니까)
그렇지 않은 경우(자식 노드로 탐색을 이어나가야 하는 경우) -> for문을 이용해 recursive하게 탐색을 이어간다.
이미 놓여진 말의 다음 말을 1~N까지의 모든 열의 위치에 넣고 답이 있는지 탐색하는 것이다.
promising 함수 구현하기
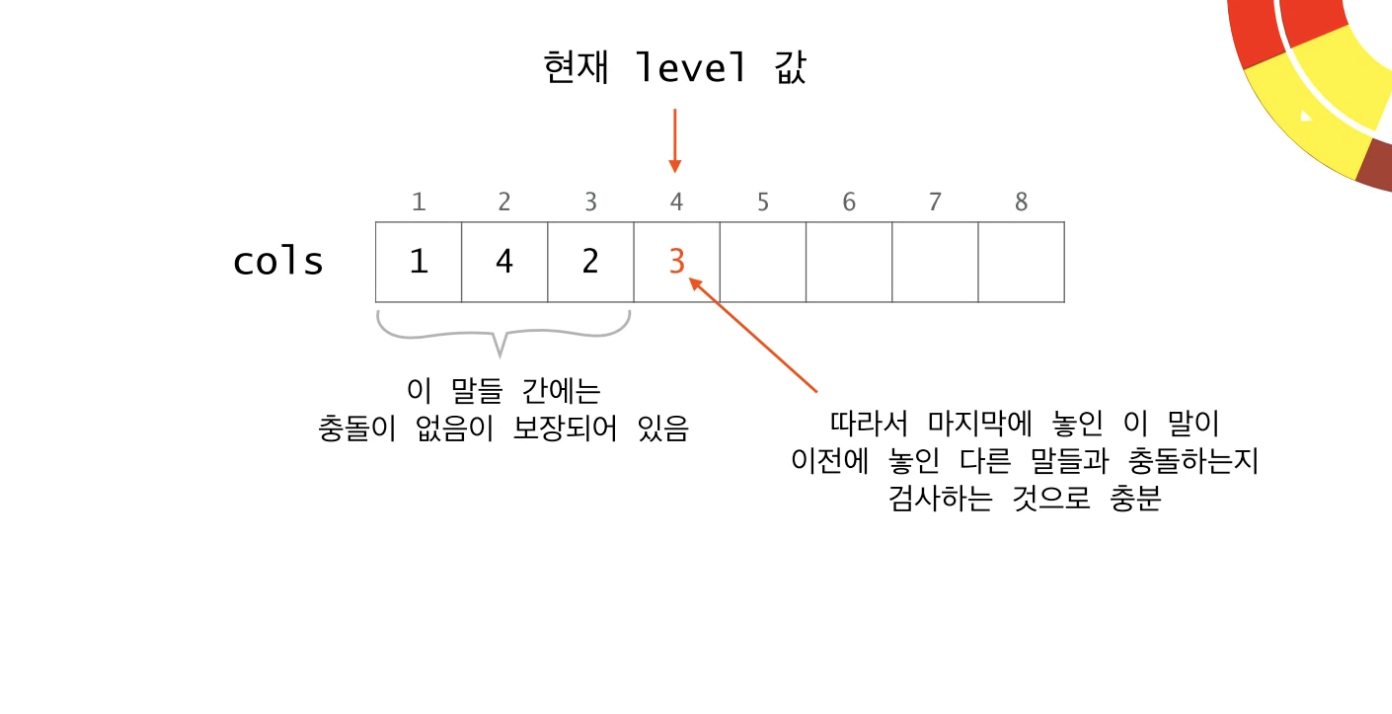
cols 배열을 인덱스=행, 값=열로 해석하면 된다.
4x4 체스판에서 (1, 1) (2, 4) (3, 2) 말이 놓여져 있고, 현재 레벨인 4에서 해가 있는지 없는지 판별하는 과정이다.
앞선 말들은 cols 배열에 들어가 있으니까 충돌이 없음이 보장된 상태라서
현재 레벨에서 말을 특정 위치에 놓았을 때 앞선 말들과 충돌이 일어나는가 일어나지 않는가 판단해
충돌이 일어난다면 non-promisig한 = 꽝!인 말로 더이상 탐색하지 않게 해주고, 충돌이 일어나지 않는다면 탐색을 이어가거나 N=level일 경우에는 답을 찾았으니 탐색을 종료하면 된다.


앞선 말들과 충돌이 일어나는 경우는 1) 같은 열에 놓였거나 2) 같은 대각선에 놓인 경우다.
1)은 이전 말들의 cols 배열 값을 현재 말의 cols 배열 값과 비교함으로써 검사할 수 있고

2)는 두 점이 대각선에 놓인 경우니까
그림처럼 두 점이 좌하향 관계에 있을 때, 두 점 사이의 가로 길이와 세로 길이가 같으면 대각선에 있다고 판단하면 된다.
level은 i의 다음 말이기 때문에 무조건 level 값이 i보다 커 level-i 값은 항상 양수이지만,
그림과 반대로 두 점이 우하향 관계에 있을 때는 우변 값이 음수이기 때문에 절댓값을 취해주어야 한다.

마지막으로 탐색이 끝난 경우에 체스판에 놓인 말들의 위치를 출력해주는 코드를 넣어 마무리.
코드
public class queens {
static int N=4;
static int[] cols = new int[N+1];
public static boolean queens(int level) {
if(!promising(level)) // 꽝인 노드의 경우
return false; // 탐색 중지. 무르기
else if(level==N) { // 그래프 맨 아래 노드까지 탐색한 경우
for (int i = 1; i <= N; i++) {
System.out.println("("+i+"," +cols[i]+")");
}
return true; // 탐색 종료.
}
else {
for (int i = 1; i <= N; i++) { // 모든 자식노드 탐색
cols[level+1] = i; // 1부터 N까지 열의 위치에 말 놓기
if(queens(level+1)) // 다음 말을 놓았다면
return true; // 계속 다음 말 놓는 동작 반복
}
return false;
}
}
public static boolean promising(int level) {
for (int i = 1; i < level; i++) {
if(cols[level] == cols[i]) // 같은 열에 놓였는지 검사
return false;
else if(level-i == Math.abs(cols[level] - cols[i])) // 같은 대각선에 놓였는지 검사
return false;
}
return true;
}
public static void main(String[] args) {
queens(0);
}
}
결과

'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 순환 (Recursion) 의 응용 : 멱집합(powerset) (0) | 2022.11.29 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #02-11 11. 임시반장 정하기 (0) | 2022.11.28 |
| [Inflearn] 자바 알고리즘 문제풀이 #02-10 10. 봉우리 (2) | 2022.11.22 |
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 순환 (Recursion) 의 응용 : Counting Cells in a Blob (0) | 2022.11.21 |
| [Inflearn] 자바 알고리즘 문제풀이 #02-09 9. 격자판 최대합 (0) | 2022.11.21 |



