멱집합 (powerset)
문제
멱집합 : 어떤 집합 A에 대하여 A의 모든 부분 집합들로 이루어진 집합

예를 들어, A : {a, b, c}라면
A의 멱집합은 ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}의 8개가 되며 원소가 n개일 때 멱집합의 개수는 2^n개이다.
(원소 하나가 포함되거나, 포함되지 않거나 2가지의 경우의 수를 가지기 때문)
알고리즘

멱집합을 recursion 방식으로 생각해보자.
이 알고리즘의 ✨✨✨✨ 가장 큰 포인트 ✨✨✨✨는
1) 원소 a를 포함한 부분집합들과 2) 원소 a를 포함하지 않는 부분집합들로 나뉜다는 것이다.
원소 a는 상황에 따라 여러 개가 될 수 있다.
위의 예시에서는 {a}, {a, b}, {a, c}, {a, b, c}가 a를 포함한 부분 집합들이 되고 ø, {b}, {c}, {b, c}가 a를 포함하지 않는 부분집합들이 된다.
1) a를 포함한 부분 집합 : {a}, {a, b}, {a, c}, {a, b, c}
2) a를 제외한 부분집합 : ø, {b}, {c}, {b, c}
1)과 2)로 멱집합을 구하는 방법은 a를 제외한 부분집합 + a를 제외한 부분집합에 a를 추가한 집합이다.
a를 제외한 부분집합은 ø, {b}, {c}, {b, c}이고,
이것에 a를 추가한 집합은 {a}, {a, b}, {a, c}, {a, b, c}이므로
이 집합들을 모두 모았을 때 {a, b, c}의 멱집합이 되는 것이다.

{b, c, d, e, f} 의 모든 부분집합들은 1) 원소 b를 포함한 부분집합들과 2) 원소 b를 포함하지 않는 부분집합들로 나뉜다.따라서 b를 제외한 {c, d, e, f}의 모든 부분집합들에 {a}를 추가한다면 2) 원소 b를 포함하지 않는 부분집합들 이 되고,
{c, d, e, f}의 모든 부분집합들에 {a, b}를 추가한다면 1) 원소 b를 포함한 부분집합들이 되는 원리이다.

위에서 설명한 것이 반복된다.
{c, d, e, f}의 모든 부분 집합은 1) 원소 c를 포함한 부분집합들과 2) 원소 c를 포함하지 않는 부분집합들로 나눌 수 있고
2)를 만드려면 {d, e, f}의 멱집합에 {a}를 추가하면 되고, 1)을 만드려면 {d, e, f}의 멱집합에 {a, c}를 추가하면 되는 것이다.
sudo code

위 코드의 문제점
1. 많은 개수의 집합들을 리턴하는 것이 간단하지 않다.
2. powerSet함수가 멱집합을 리턴하지 않고 출력만 한다면 poswerSet(S-{t})의 결과에 t를 추가한 부분집합을 출력할 수가 없다.
(리턴된 결과에 t를 붙여 원하는 다음 결과를 얻어야 하는데 그것이 불가능해짐)

그래서, 앞서 말했던 알고리즘처럼 어떤 원소 t에 대하여
powerSet(P, S-{t}) : t를 제외한 모든 부분집합들
powerSet(PU{t}, S-{t}) : t를 포함한 모든 부분집합들
두 가지로 나눠 결과과 나왔을 때 출력하면 된다.

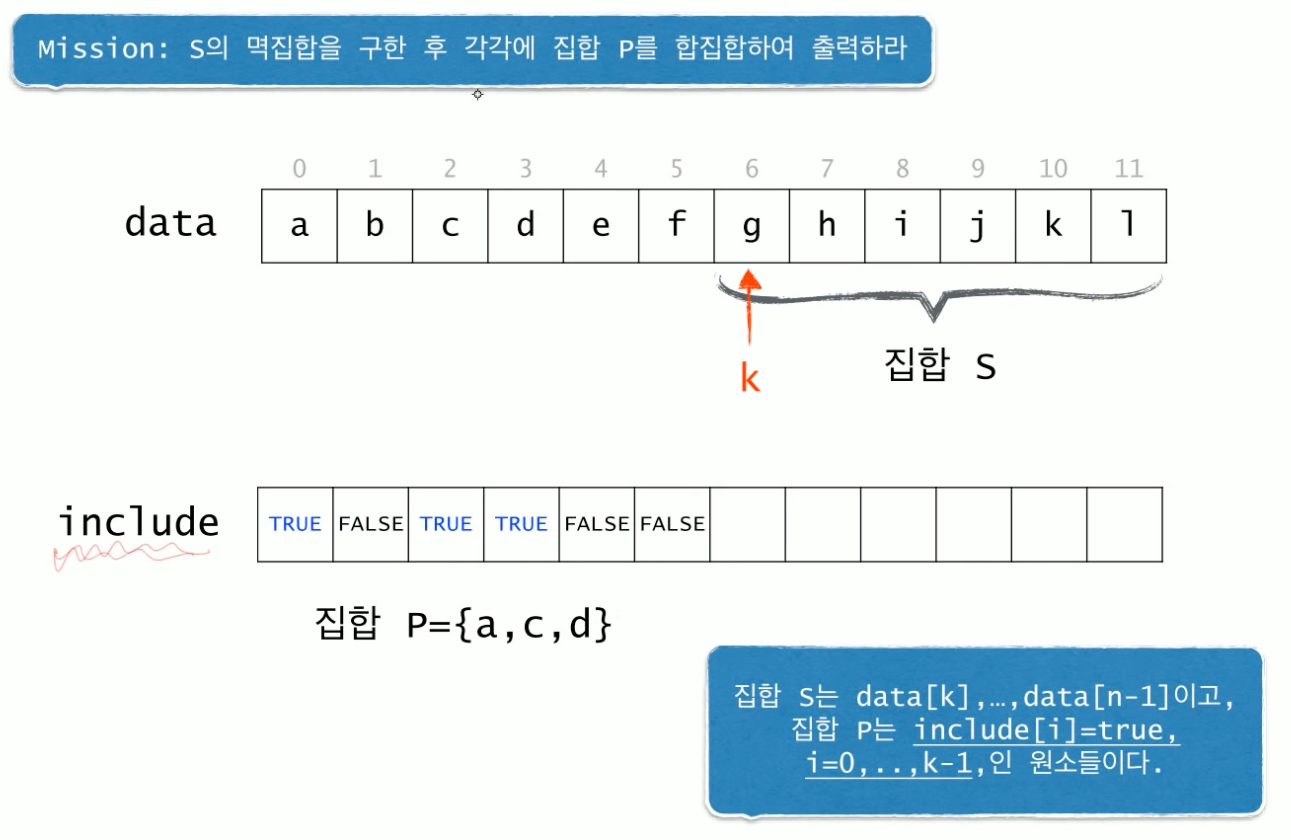
여기서 집합 S는 k번째 원소부터 마지막 원소까지 연속된 원소들이고, 집합 P는 처음부터 k-1번째 원소들 중 일부가 된다.
코드상에서 본다면 집합 S는 data 배열의 k번째 배열부터 n-1 배열까지를 나타내고,
집합 P는 data의 0번째 배열부터 k-1번째 배열 중 include 배열에서 true 값을 갖는 원소들을 나타내기로 하자.
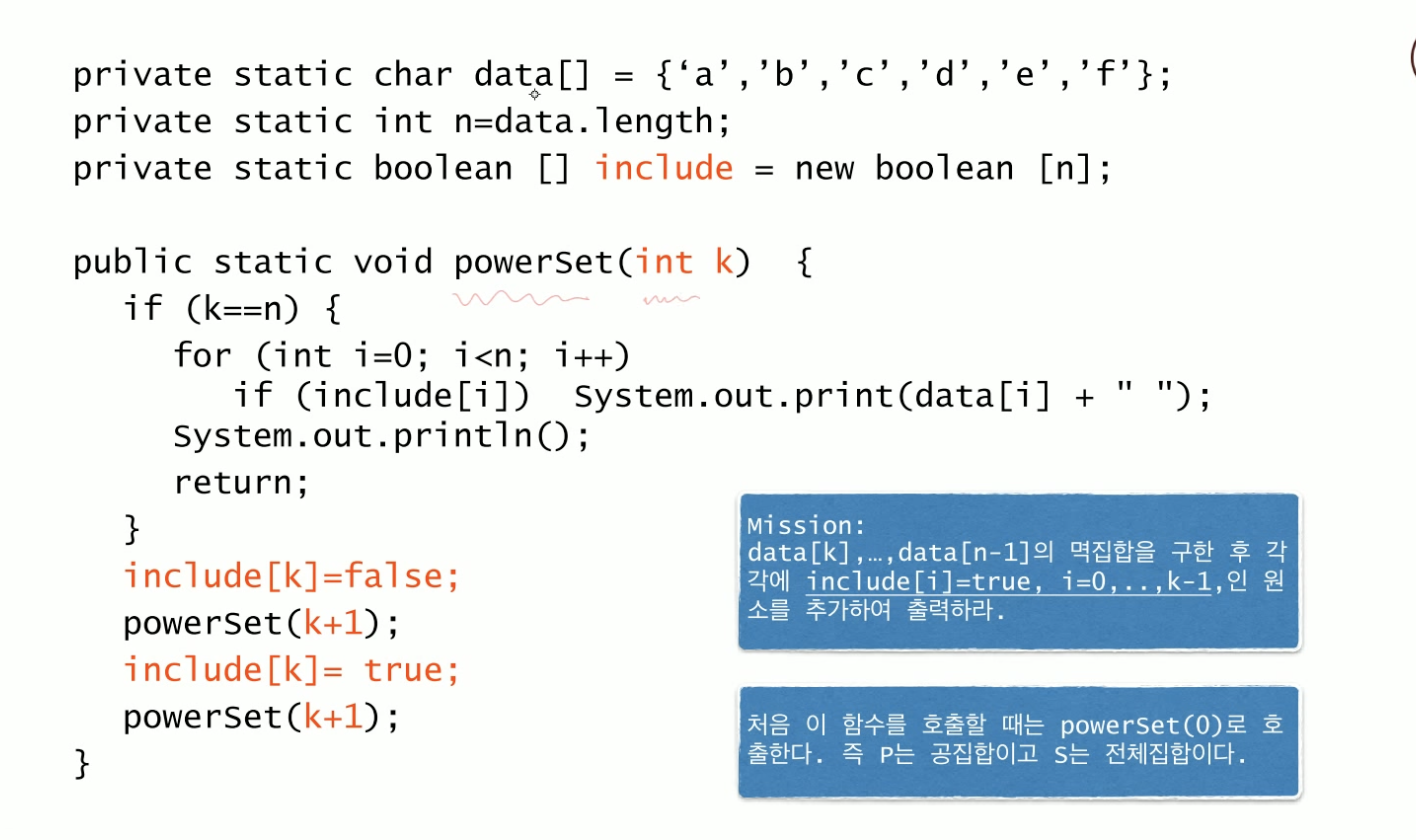
Base case (순환을 멈추는 조건) : k가 data 배열을 다 돌아 n이 될 때 = 집합 S가 공집합이 될 때
powerSet 함수의 역할
- recursive case : 집합 S의 모든 부분집합들을 구해 P를 합쳐서 출력 ==> 1) 어떤 원소 P가 포함된다 ==> include에서 true인 알파벳들이 포함된다
- base case : P를 출력 ==> 2) 어떤 원소 P가 포함되지 않는다
✨✨핵심코드✨✨
- include[k]=false;
powerSet(k+1); : 원소 k를 포함하지 않는 원소들의 부분집합들을 출력
- include[k]=true;
powerSet(k+1); : 원소 k를 포함하는 원소들의 부분집합들을 출력
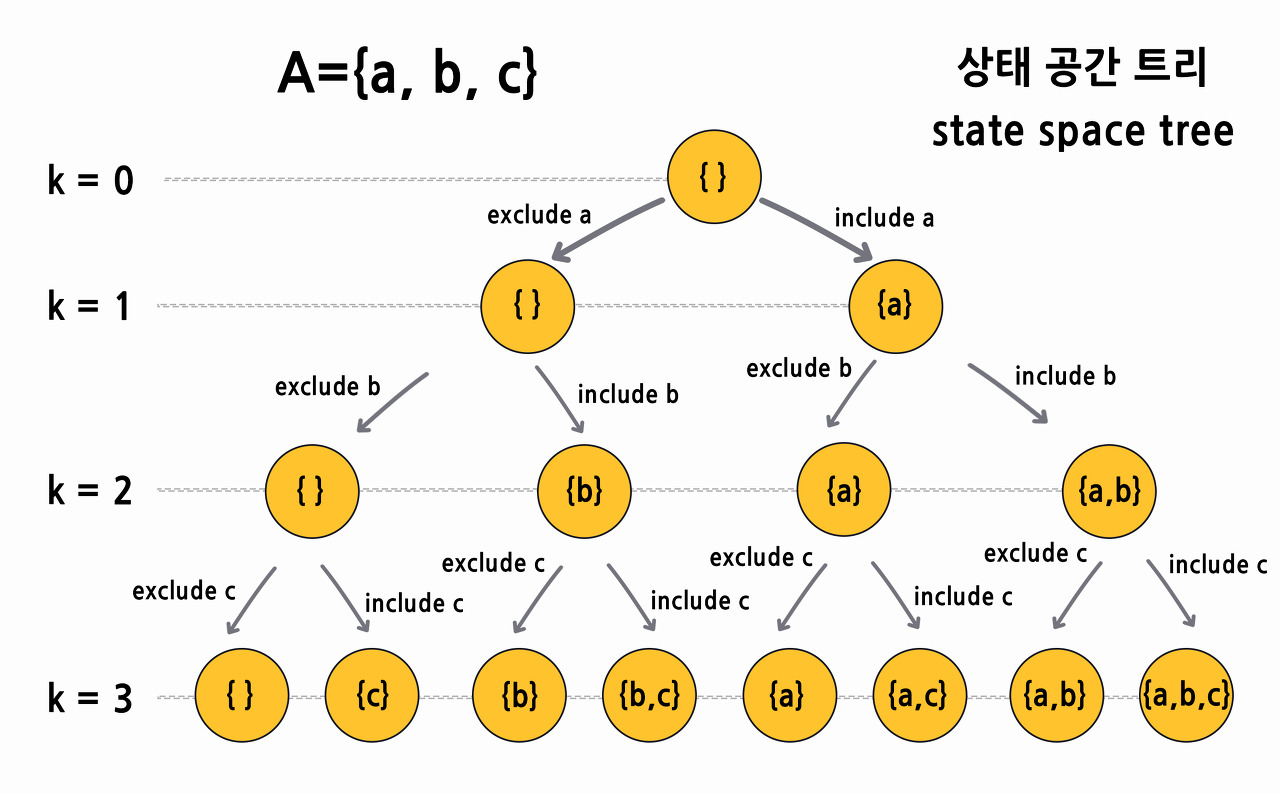
반복적으로 powerSet 함수를 호출하며 상태공간트리를 만들어 가며 가장 아래 level에서 정답을 도출한다.
원소 a가 빠졌을 때, 원소 b가 빠졌을 때, 원소 c가 빠졌을 때, 원소 a, b가 빠졌을 때, 원소 a, c가 빠졌을 때, 원소 b, c가 빠졌을 때, 원소 a, b, c가 빠졌을 때의 모든 상황을 규칙적으로 가지치기하며 탐색하는 것이다.
상태공간트리란 ?
- 해를 찾기 위해 탐색할 필요가 있는 모든 후보들을 포함하는 트리
- 트리의 모든 노드들을 방문하면 해를 찾을 수 있다
- 루트에서 출발하여 체계적으로 모든 노드를 방문하는 절차를 기술한다.
이전 시간에 했던 n queens problem 에서도 나왔던 개념이다.
n queens problem은 모든 경로를 탐색하지 않고, 중간에 꽝인 노드라면 그 아래로는 탐색을 중단했는데,
powerset 문제는 모든 리프 노드까지 탐색을 마쳐야 정답을 구할 수 있다

상태 공간 트리로 생각하면 핵심 코드의 의미가 확장된다.
✨✨핵심코드✨✨
- include[k]=false;
powerSet(k+1); : 원소 k를 포함하지 않는 원소들의 부분집합들을 출력 ==> exclude인 왼쪽 노드를 타고 내려가는 것
- include[k]=true;
powerSet(k+1); : 원소 k를 포함하는 원소들의 부분집합들을 출력 ==> include인 오른쪽 노드를 타고 내려가는 것
코드
public class powerSet {
private static char data[]= {'a','b','c','d'};
private static int n=data.length;
private static boolean[] include = new boolean[n];
public static void powerSet(int k) {
if(n==k) {
for(int i=0;i<n;i++) {
if(include[i]) System.out.print(data[i]+" ");
}
System.out.println();
return;
}
include[k]=false;
powerSet(k+1);
include[k]=true;
powerSet(k+1);
}
public static void main(String[] args) {
powerSet(0);
}
}
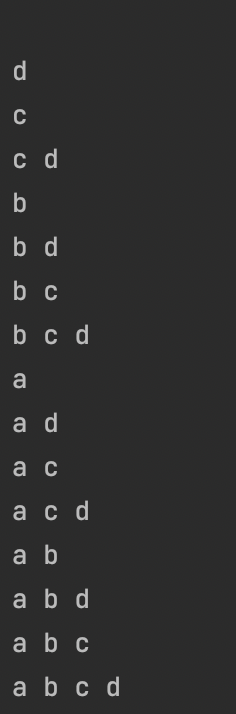
결과
'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 자바 알고리즘 문제풀이 #03-01 1. 두 배열 합치기 (0) | 2022.12.13 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #02-12 12. 멘토링 (0) | 2022.11.29 |
| [Inflearn] 자바 알고리즘 문제풀이 #02-11 11. 임시반장 정하기 (0) | 2022.11.28 |
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 순환 (Recursion) 의 응용 : n queens problem (0) | 2022.11.22 |
| [Inflearn] 자바 알고리즘 문제풀이 #02-10 10. 봉우리 (2) | 2022.11.22 |



