힙 정렬 (heap sort)
지난 시간 빠른 정렬(quick sort)에 대해 배웠다.
https://rookie-programmer.tistory.com/56
[Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 빠른 정렬 (quick sort)
빠른 정렬 (quick sort) 지난 시간 합병 정렬에 대해 배웠다. https://rookie-programmer.tistory.com/54 [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 합병 정렬 (merge sort) 합병 정렬 (merge sort) 지난 시간에 버블
rookie-programmer.tistory.com
이번 시간에는 힙 정렬 (heap sort)에 대해 배운다.

합병 정렬에서는 추가 배열을 사용했을 때 최악의 경우 시간복잡도가 O(n logn)이었지만
힙 정렬은 추가 배열을 사용하지 않고, 주어진 배열만을 사용해 정렬이 가능하다.
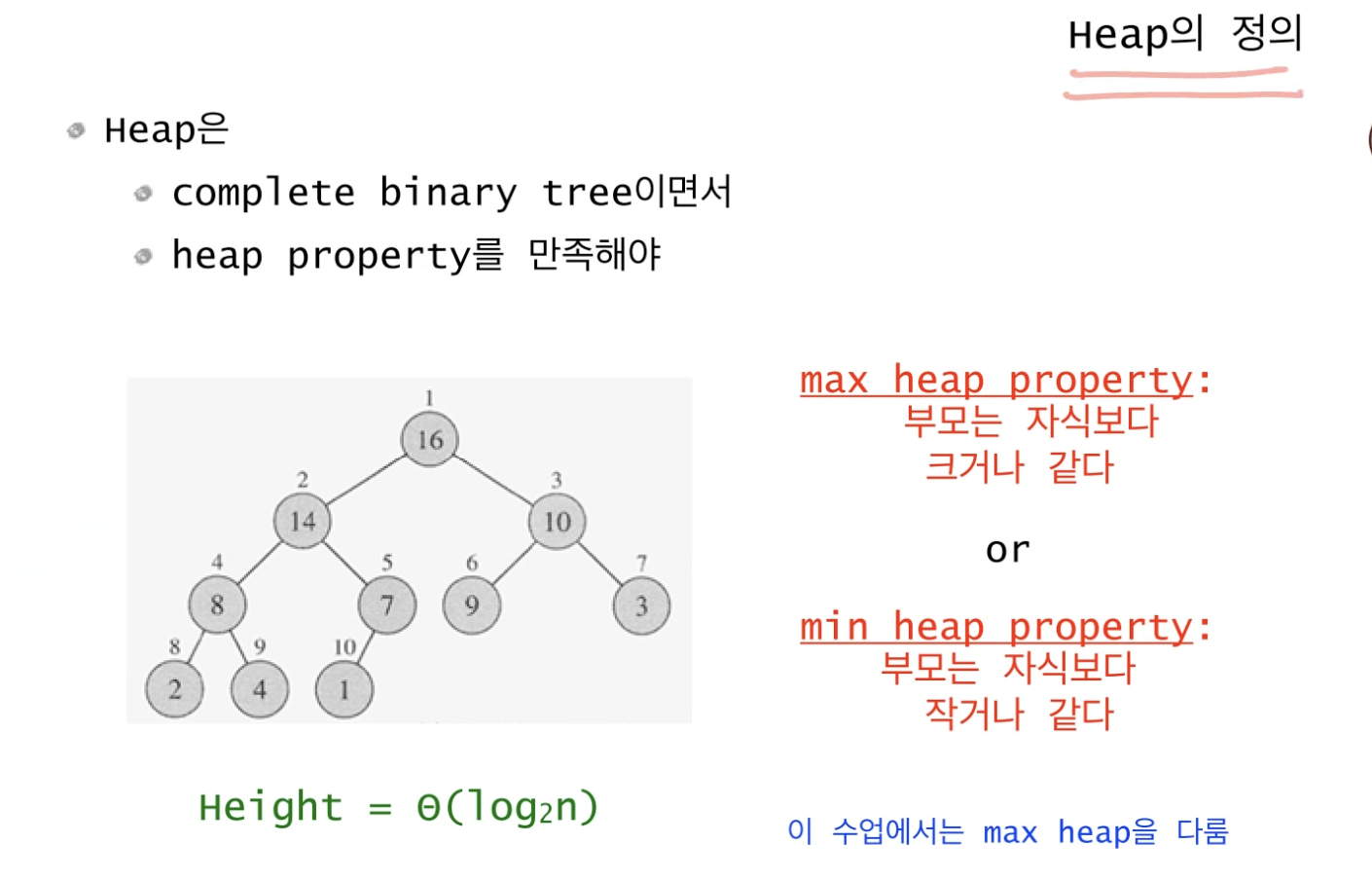
힙(Heap) 정렬에서 힙이라는 것은 두 가지 조건을 만족시켜야 한다.
1. 완전이진트리이면서 (이진트리 = 자식 노드가 최대 2개인 트리)
2. 부모가 자식보다 크거나 같은 max 혹은 부모가 자식보다 작거나 같은 min의 특징을 가져야 한다.
보통 min heap보다는 max heap을 사용한다.
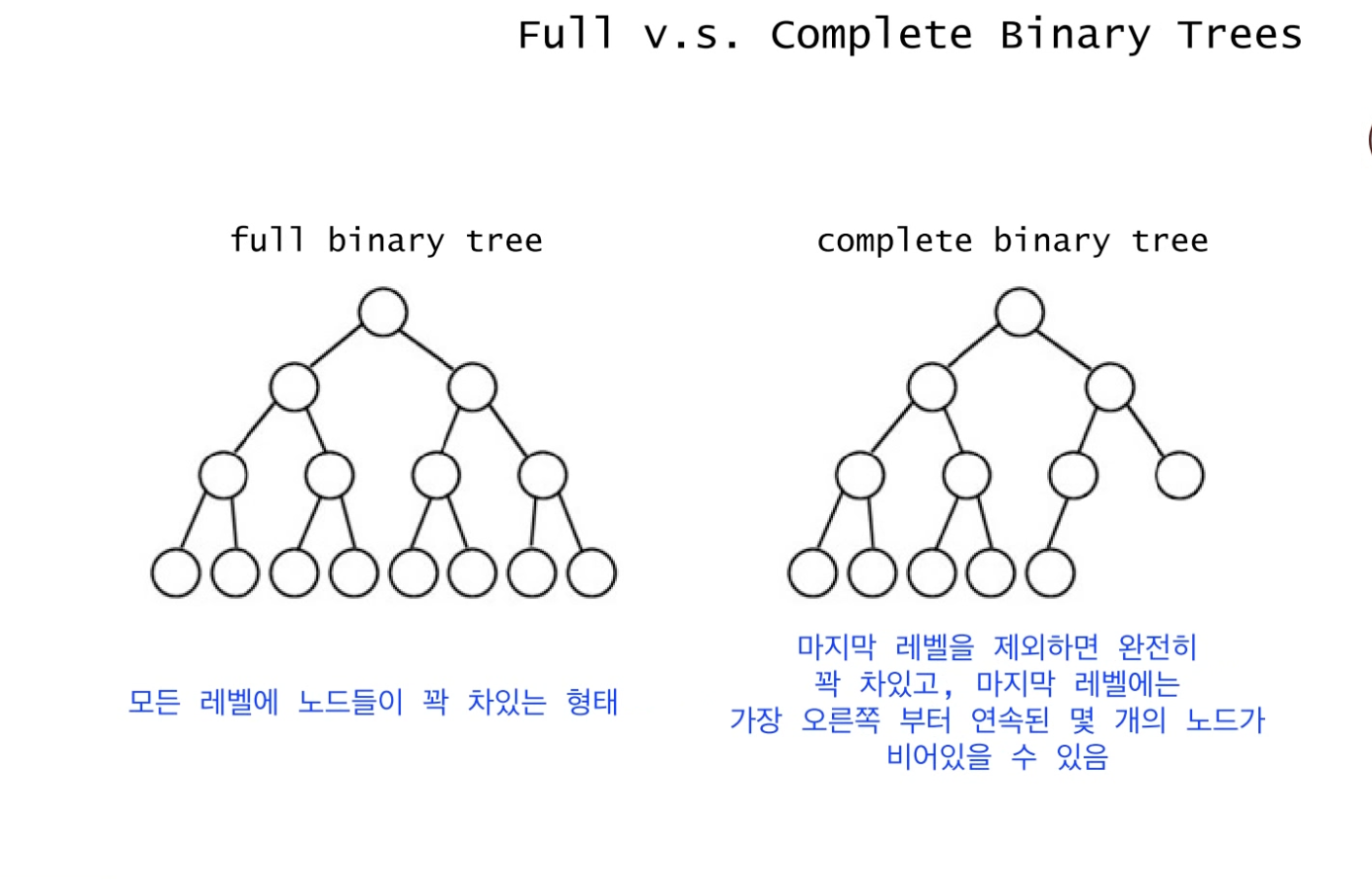
이진 트리의 종류는 포화 이진트리, 완전 이진트리, 편향 이진트리가 있다.
포화 이진트리(full binary tree)와 완전 이진트리(complete binary tree)의 차이점은
포화 이진트리는 트리의 모든 레벨에 노드들이 꽉 차있는 형태로, 각 레벨에서 가질 수 있는 최대 노드의 수를 가지는 트리이다.
완전 이진트리는 마지막 레벨을 제외한 레벨에는 꽉 차있지만, 마지막 레벨은 꽉 차있지 않아도 된다.
하지만, 마지막 레벨은 무조건 왼쪽 노드부터 차례대로 채워져야 한다. (중간에 이빨 빠질 수 없다!)
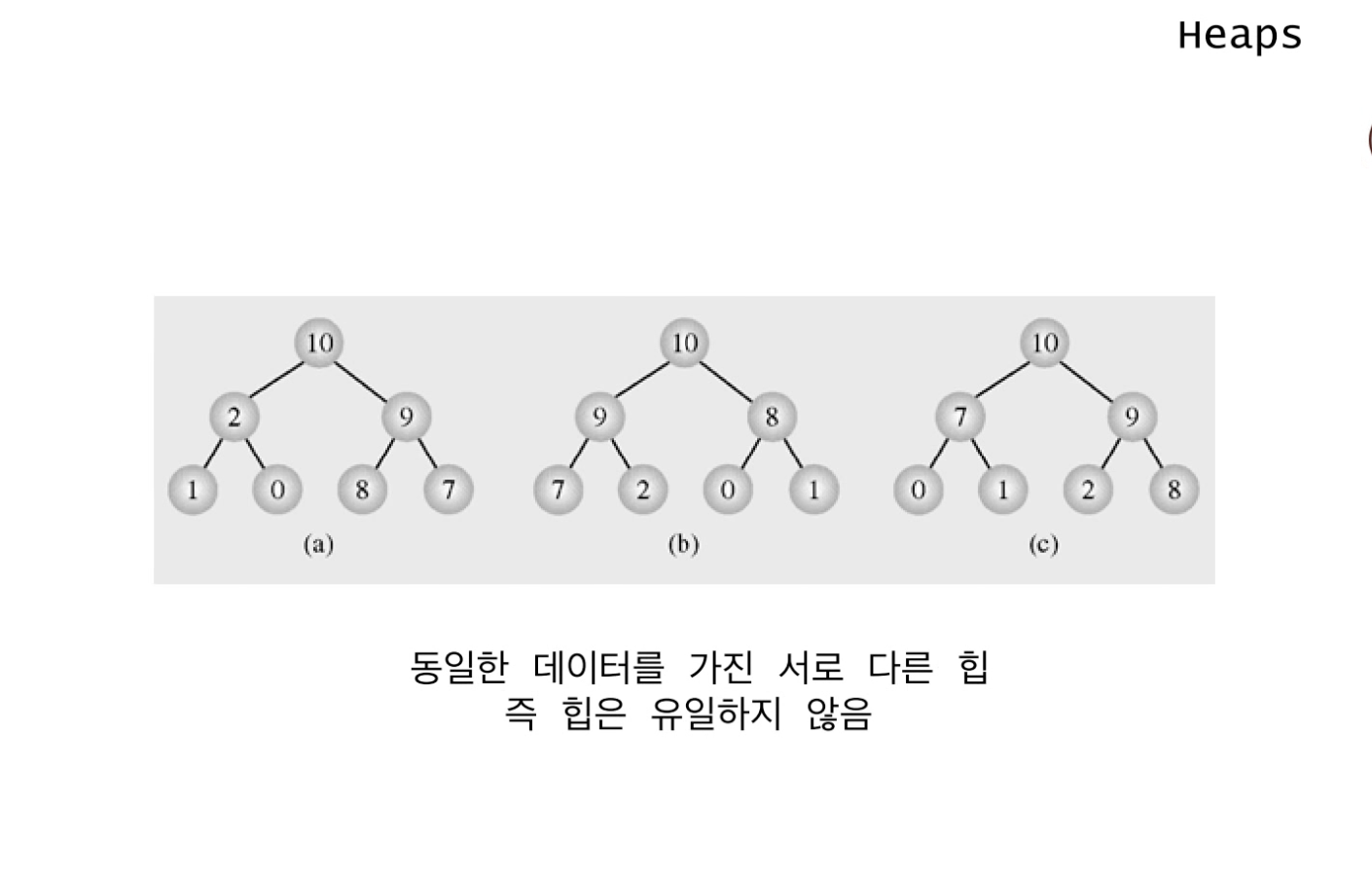
(a), (b), (c) 모두 위의 1. 2. 조건을 만족하므로 힙이 될 수 있다.
0, 1, 2, 7, 8, 9, 10 7개의 데이터로 여러 개의 힙을 만들 수 있다. = 힙은 유일하지 않다.
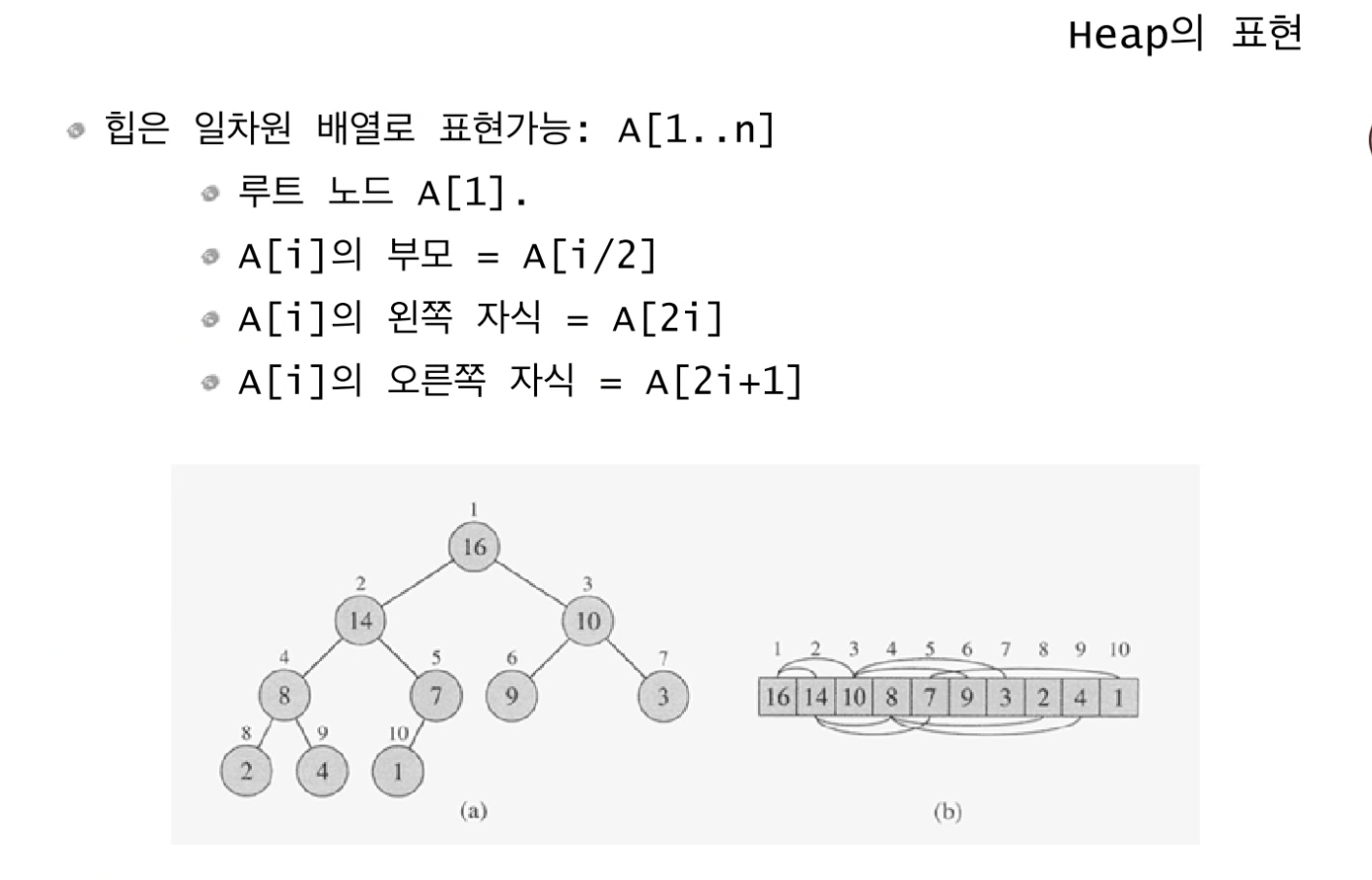
힙은 위와 같은 성질을 가지며 일차원 배열로 표현될 수 있다.
인덱스 1번을 가지는 "16"의 왼쪽 자식은 인덱스 2x1=2번으로 그 값은"14", 오른쪽 자식은 2x1+1=3번으로 값은"10"이다.
Heap으로 만드는 과정 ⭐️⭐️⭐️⭐️⭐️
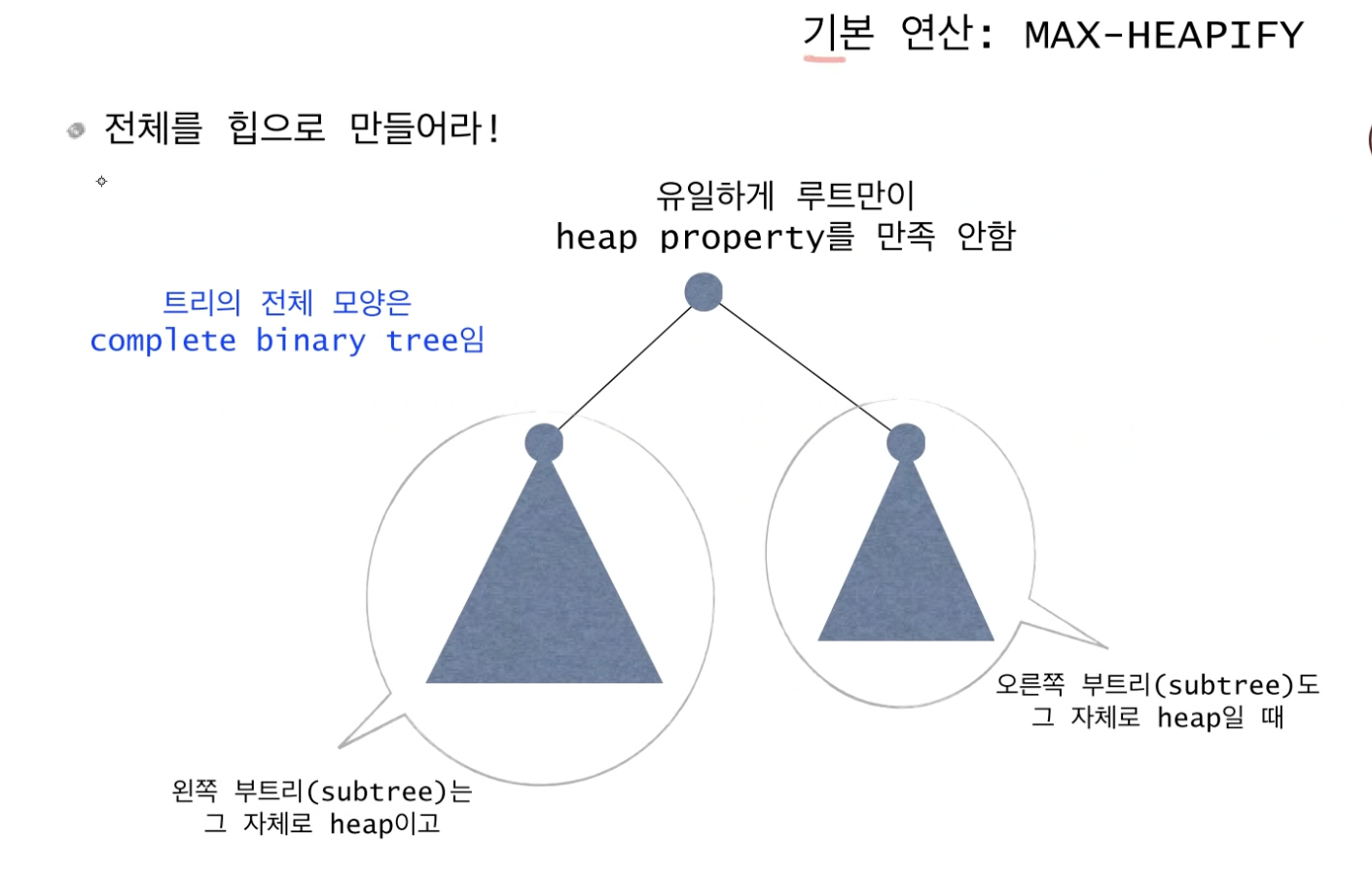
왼쪽 자식 노드를 root로 하는 왼쪽 부트리는 heap이고, 오른쪽 자식 노드를 root로 하는 오른쪽 부트리도 heap인데
root 노드만 heap property를 만족하지 않을 경우 (부모 노드가 자식 노드보다 크거나 같은 값을 가지고 있지 않을 경우)
전체 트리를 Heap으로 만드는 역할을 하는 함수를 MAX-HEAPIFY라고 부르자.
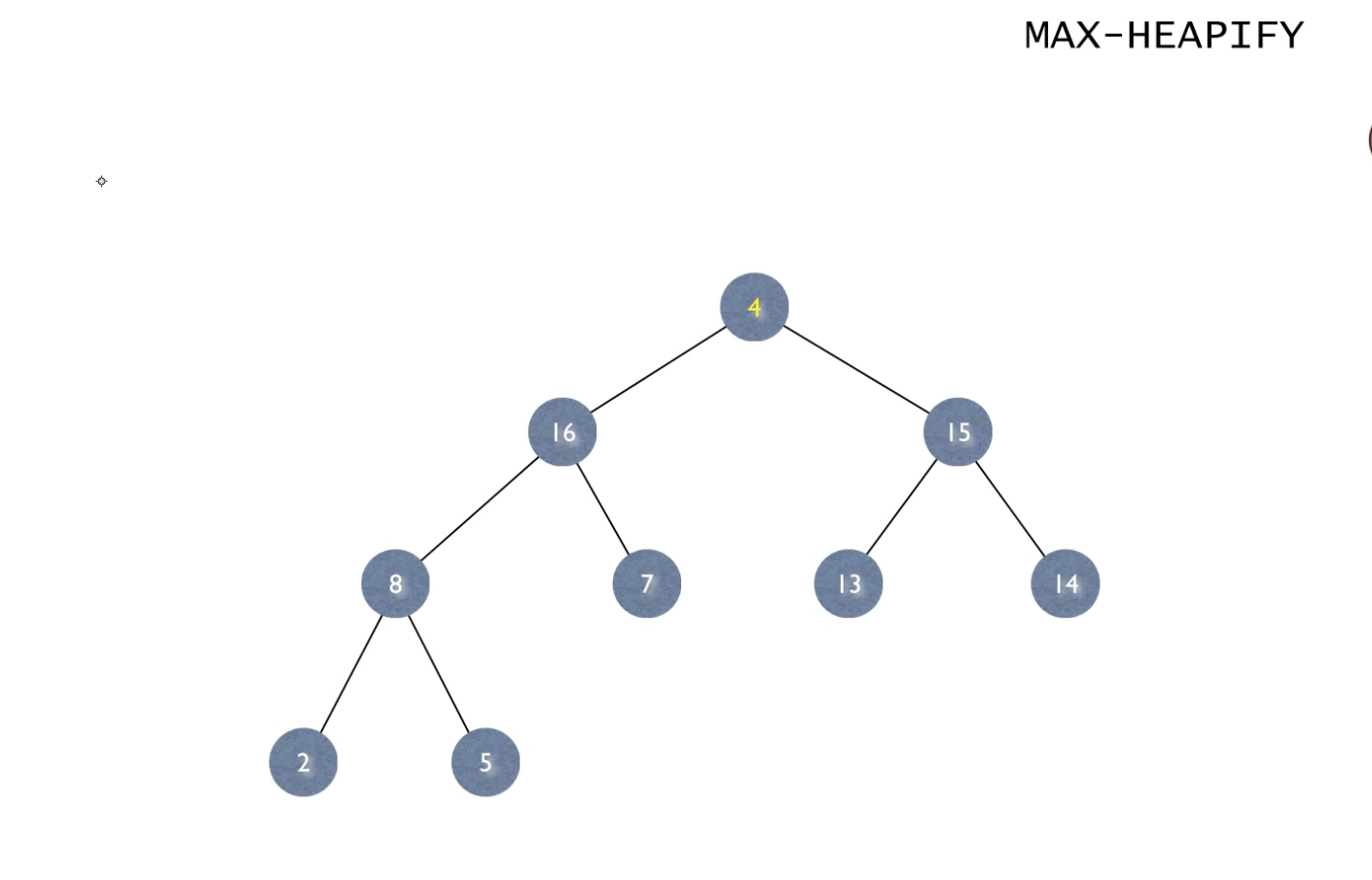
예를 들어, 아래의 상황에서
16을 루트 노드로 하는 왼쪽 부트리는 heap 성질을 모두 만족하고 있고,
15를 루트 노드로 하는 오른쪽 부트리도 heap 성질을 모두 만족하고 있지만
가장 상위 노드인 root 노드의 값이 "4"로 그 자식 노드 "16", "15"보다 작은 값을 가져 트리 전체는 heap이 되지 않는다.
이럴 때 해결 방법은 자식 노드 중 더 큰 쪽과 root노드를 바꾸는 과정을 반복하는 것이다.
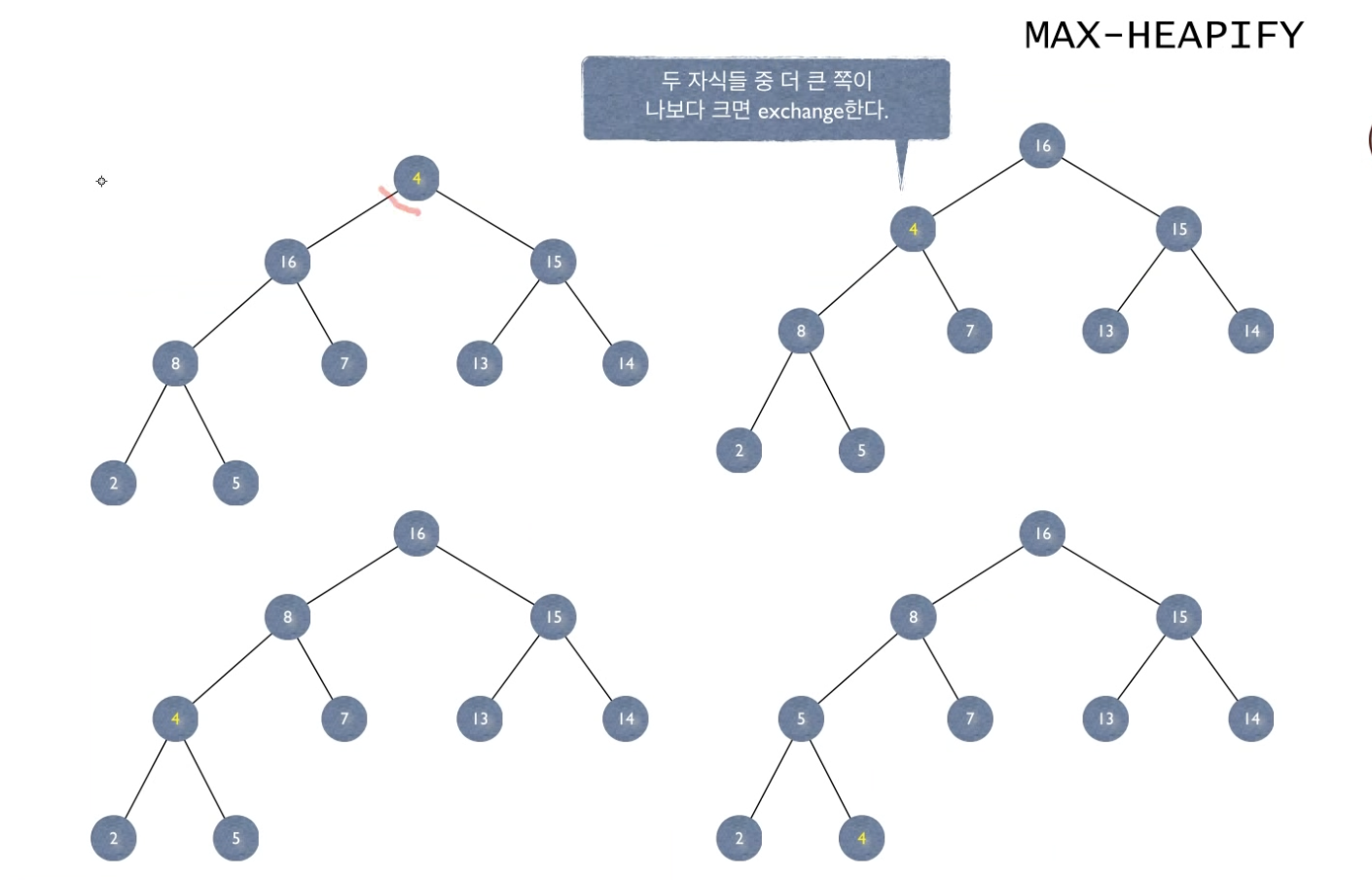
4의 자식 노드 15, 16 중 큰 수인 16과 4가 자리를 바꿔 두 번째 그림이 되고
두 번째 줄로 내려온 4의 자식 노드 7, 8 중 큰 수인 8과 4가 자리를 바꿔 세 번째 그림이 되고
세 번째 줄로 내려온 4의 자식 노드 2, 5 중 큰 수인 5와 4가 자리를 바꿔 마지막 그림이 된다.
이렇게 자식 노드 중 더 큰 쪽과 root노드를 바꾸는 과정을 반복하는 것이 끝나면 전체 트리는 "Heap" 성질을 만족하게 된다.
MAX-HEAPIFY의 sudo code - recursive version

자식 노드 중 더 큰 쪽과 root노드를 바꾸는 과정을 recursive하게(재귀호출) 진행한다.
MAX-HEAPIFY의 sudo code - iterative version

자식 노드 중 더 큰 쪽과 root노드를 바꾸는 과정을 반복문을 사용해서 진행한다.
아래 그림의 예제를 따라 로직을 따라가 보길 바란다.
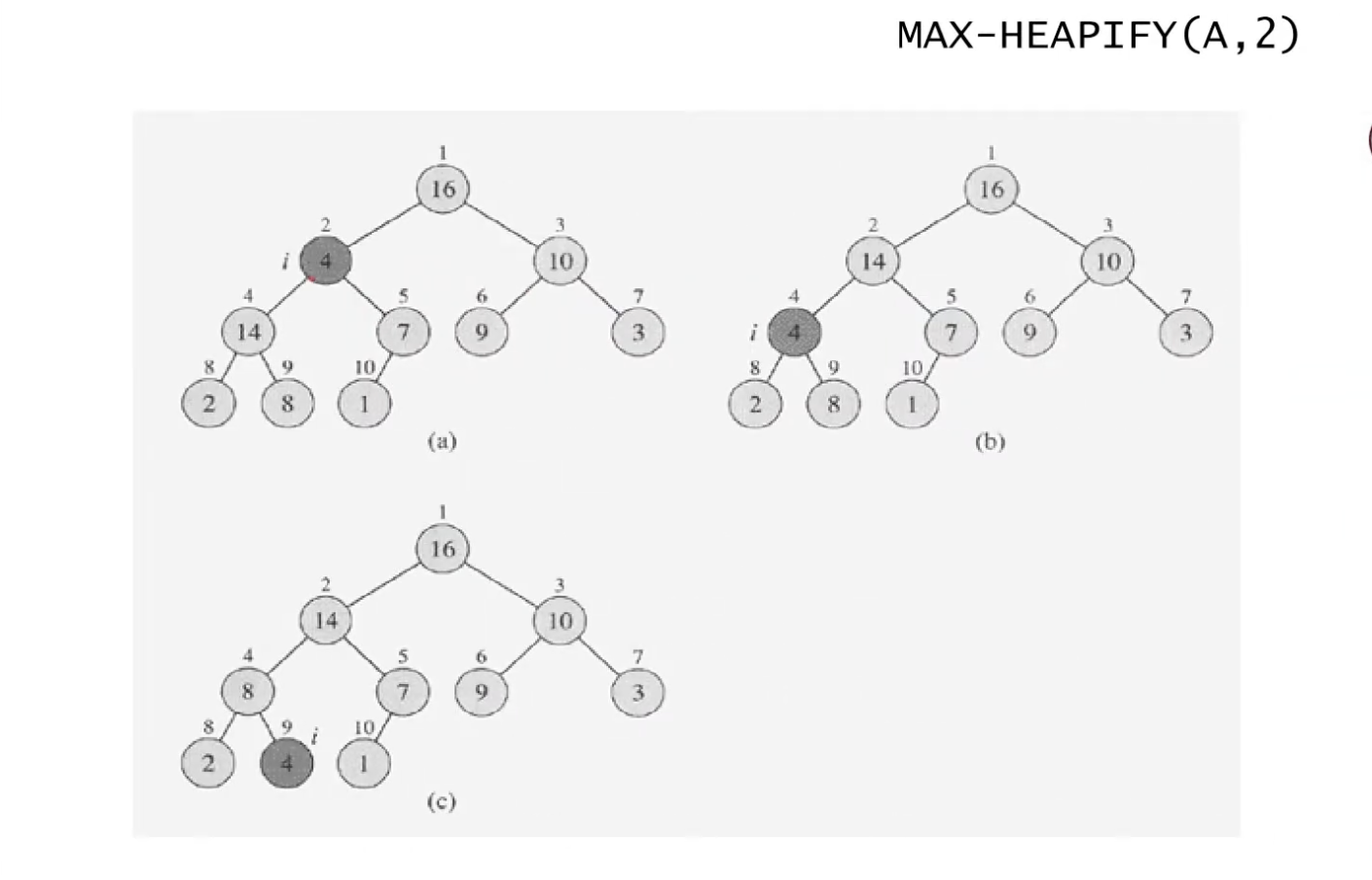
위의 예제들은 root 노드부터 내려오면서(인덱스 1번부터 시작해 n번까지) heapify를 진행했지만
아래 예제들은 마지막 레벨의 마지막 노드부터 올라가면서(인덱스 n/2번부터 시작해 1번까지) heapify를 진행한다.
인덱스 n/2번부터 시작하는 이유는 "자식 노드가 하나 혹은 두개 있는 노드"를 대상으로 해야 왼쪽 부트리 혹은 오른쪽 부트리가 있어 값을 바꿀 대상 노드가 존재하기 때문이다.

heapify를 한 번 하는데 걸리는 시간 = log n (트리의 깊이) + 1에서 n/2까지 n/2번 반복하니까 힙을 만드는데 걸리는 시간복잡도는 O(n logn)이어야 하는데, 이는 굉장히 타이트한 계산이다.
왜냐하면 heapify를 한 번 하는데 걸리는 시간 = log n은 트리의 모든 레벨을 돌아야 하는 root 노드에 대한 시간이기 때문이다.
상대적으로 나머지 서브 트리들은 그 깊이가 짧기 때문에 log n 만큼의 시간이 소요되지 않는다.
따라서 전체적으로 시간을 더해봤을 때는 힙을 만드는데 걸리는 시간복잡도는 O(n)이 된다.
(힙을 만드는데 걸리는 시간복잡도가 O(n)이라고 해도 힙 정렬에 걸리는 시간복잡도는 O(n logn)이니 혼동하지 말자)
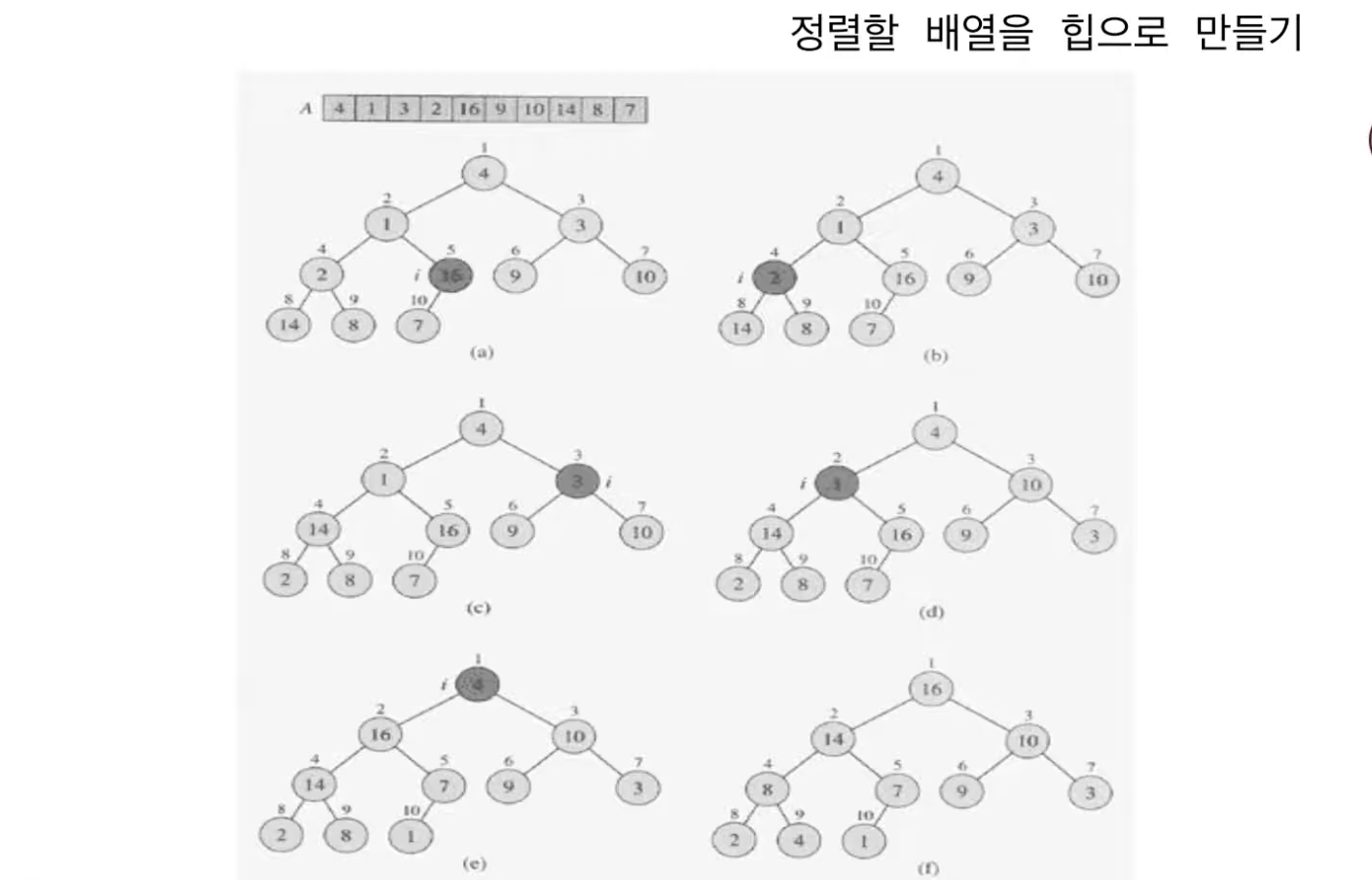
위 그림에서 10, 9, 8, 7, 6 인덱스의 노드들은 자식 노드가 하나도 없기 때문에 heapify를 진행할 수 없다.
n/2 지점인 5번 노드에서부터 1번 노드까지 heapify를 반복해 최종 (f)의 결과를 얻을 수 있다.
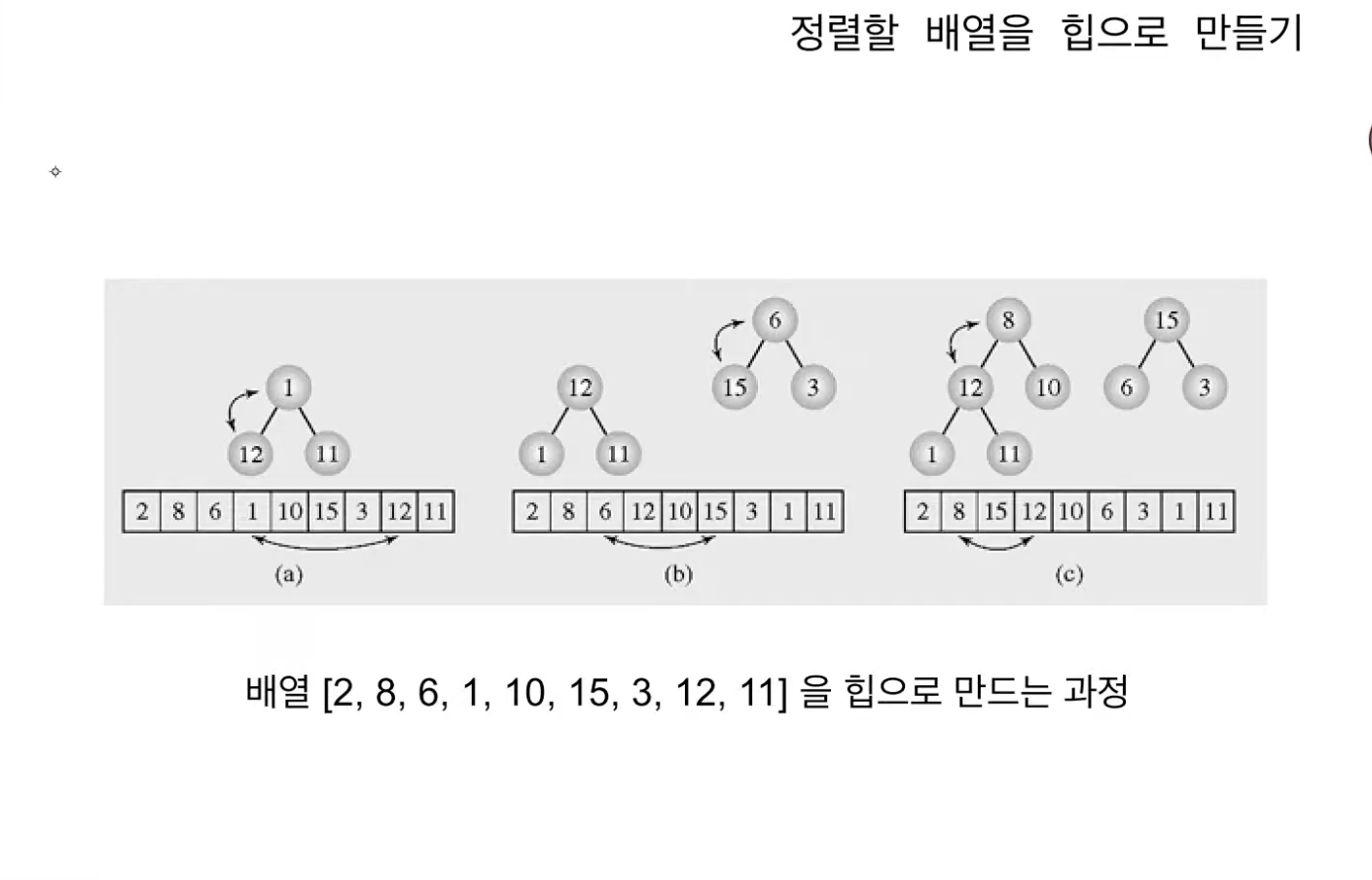
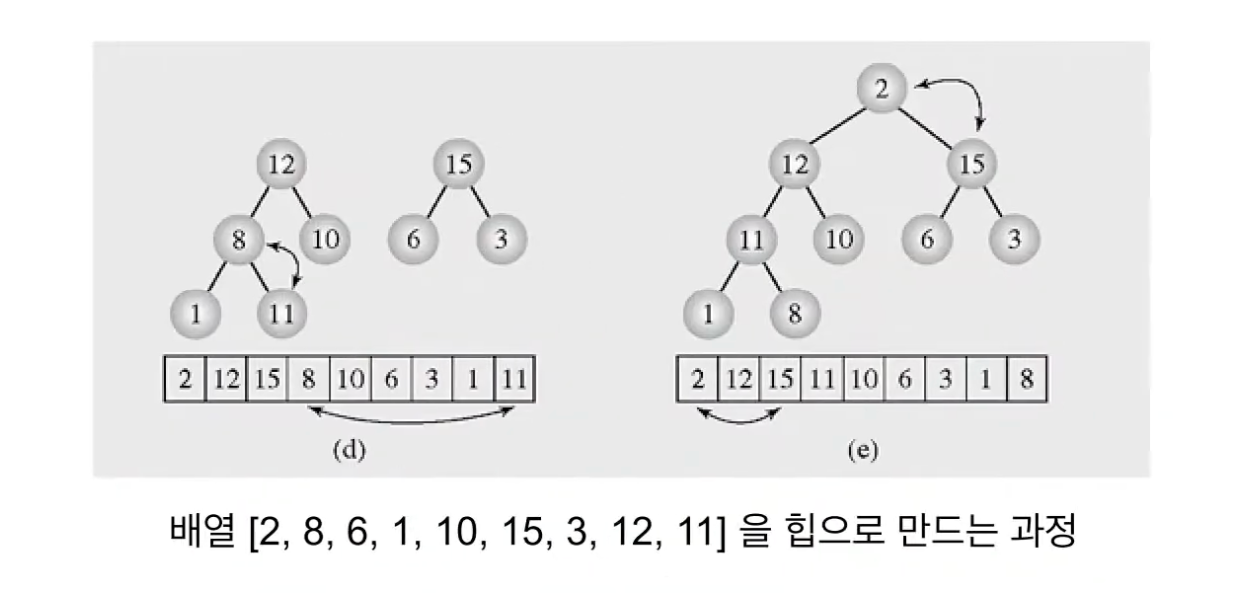
n/2 = 4이기 때문에 배열의 4번째 값인 8부터 1번째 값까지 차례대로 heapify를 진행한다.
최종 (e)의 결과를 얻을 수 있다.
==> 지금까지 heap sort에 필요한 가장 큰 개념인 "배열을 힙으로 만들기"에 대해 알아보았다.
이제 이렇게 만든 배열로 어떻게 정렬을 하는지 알아보자.
Heapsort

위에서 배웠던 주어진 배열로 힙을 만든 과정에서 주목해야 할 점이 있다.
"루트 노드는 그 배열의 최대값이 된다"는 것이다. (부모 노드는 자식 노드보다 커야되니까 당연한 일임)
그래서 힙을 만들어서 루트 노드를 최대값으로 만들어놓고, 그 최대값을 뺀 나머지 값들로 다시 힙을 만들면 루트 노드가 그 중 최대값이 된다. 이런식으로 최대값을 찾는 과정을 반복하면 가장 큰 값부터 작은 값까지 나열된 결과를 얻을 수 있다.
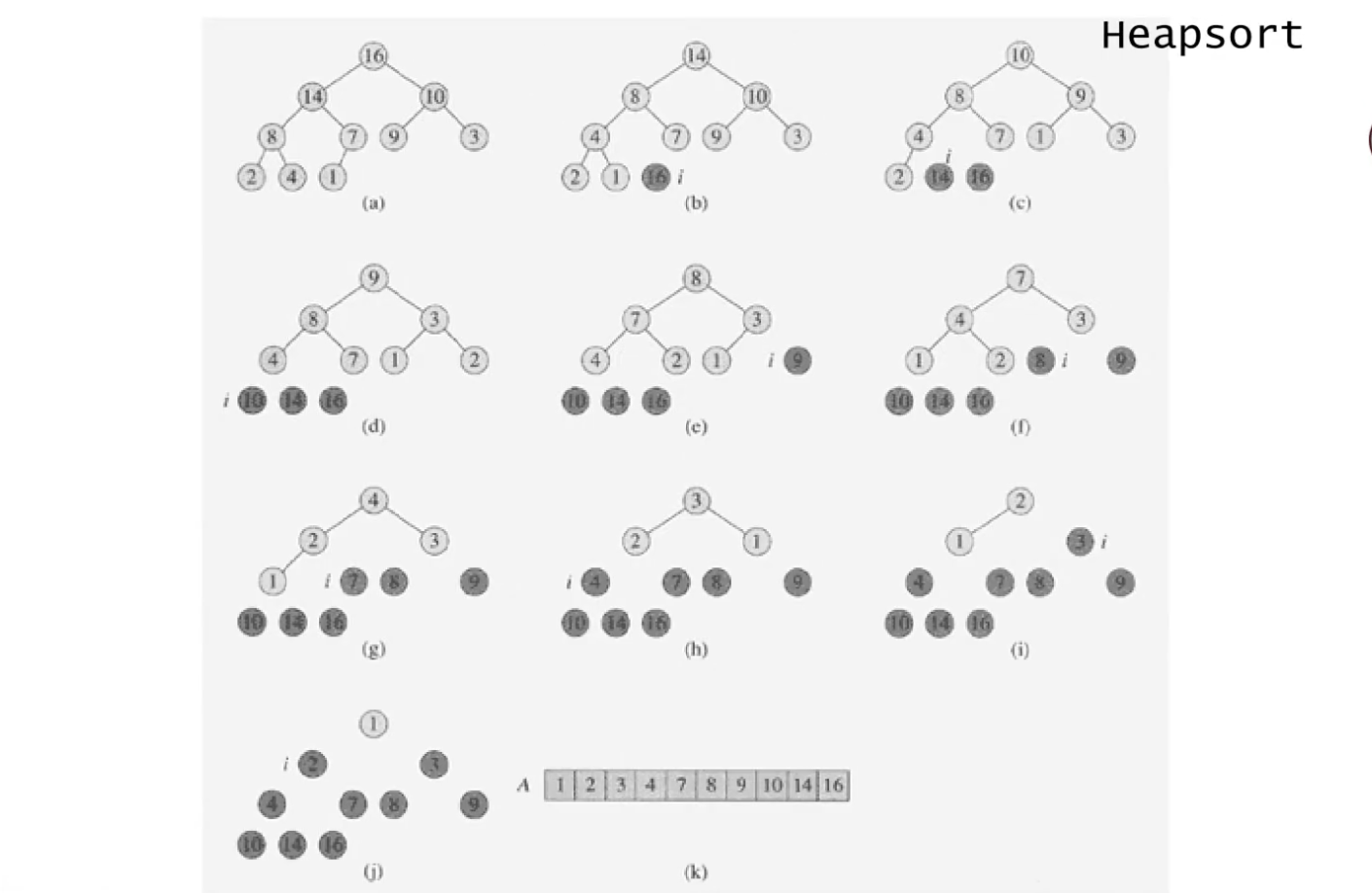
heap인 상태인 (a)에서 루트 노드인 16과 마지막 노드인 1을 바꿔, 16을 제외한 노드들에 대해 heapify를 진행한다 -> (b)가 됨
(b)에서 루트 노드인 14와 마지막 노드인 1을 바꿔, 14를 제외한 노드들에 대해 heapify를 진행한다 -> (c)가 됨
이 과정을 반복하다 보면 완전 이진트리에 값이 순차적으로 저장되는 것을 볼 수 있다. ===> HeapSort !!
* 퀵 정렬의 시간복잡도 : O(n logn)

힙으로 만드는 과정은 log n의 시간이 걸리는데 이 과정을 n-1번 반복한다.
'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 힙(heap)의 다른 응용: 우선순위 큐 (priority queue) (0) | 2023.01.12 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #04-03 3. 매출액의 종류(Hash, sliding window) (0) | 2023.01.11 |
| [Inflearn] 자바 알고리즘 문제풀이 #04-02 2. 아나그램(해쉬) (0) | 2023.01.07 |
| [Inflearn] 자바 알고리즘 문제풀이 #04-01 1. 학급 회장(해쉬) (0) | 2023.01.06 |
| [Inflearn] 자바 알고리즘 문제풀이 #03-06 6. 최대 길이 연속부분수열 (0) | 2022.12.19 |



