우선순위 큐 (priority queue)
저번 시간 힙 정렬에 대해서 배우면서 heap에 대해 배웠다.
https://rookie-programmer.tistory.com/63
[Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 힙 정렬 (heap sort)
힙 정렬 (heap sort) 지난 시간 빠른 정렬(quick sort)에 대해 배웠다. https://rookie-programmer.tistory.com/56 [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 빠른 정렬 (quick sort) 빠른 정렬 (quick sort) 지난 시간
rookie-programmer.tistory.com
힙이라는 것은 두 가지 조건을 만족시켜야 한다.
1. 완전이진트리이면서 (이진트리 = 자식 노드가 최대 2개인 트리)
2. 부모가 자식보다 크거나 같은 max 혹은 부모가 자식보다 작거나 같은 min의 특징을 가져야 한다.

(a)는 max 힙이고 힙은 (b)와 같이 1차원 배열로 나타낼 수 있고,
아래와 같은 특징을 지닌다.

힙을 이용해 "우선순위 큐"를 만들 수 있다.

어렵게 적혀있지만 최대 우선순위 큐라는 가정하에,
우선순위 큐는 MAX-HEAP에서 root 노드(최대값)들을 차례대로 뽑아내는 것이다.
그 다음 현 최대값인 root 노드를 제외한 후, 맨 마지막 레벨의 맨 오른쪽 (배열 상 가장 마지막 인덱스의 값) 값을 root로 올려준 후
MAX_HEAP을 만들고 다음 최대값인 root 노드를 뽑아낸다. 이 과정을 반복해주면 된다.
최대 우선순위 큐 (max priority queue)는 두 가지 행동을 할 수 있다.
1. 새로운 원소를 삽입
2. 최대값 반환
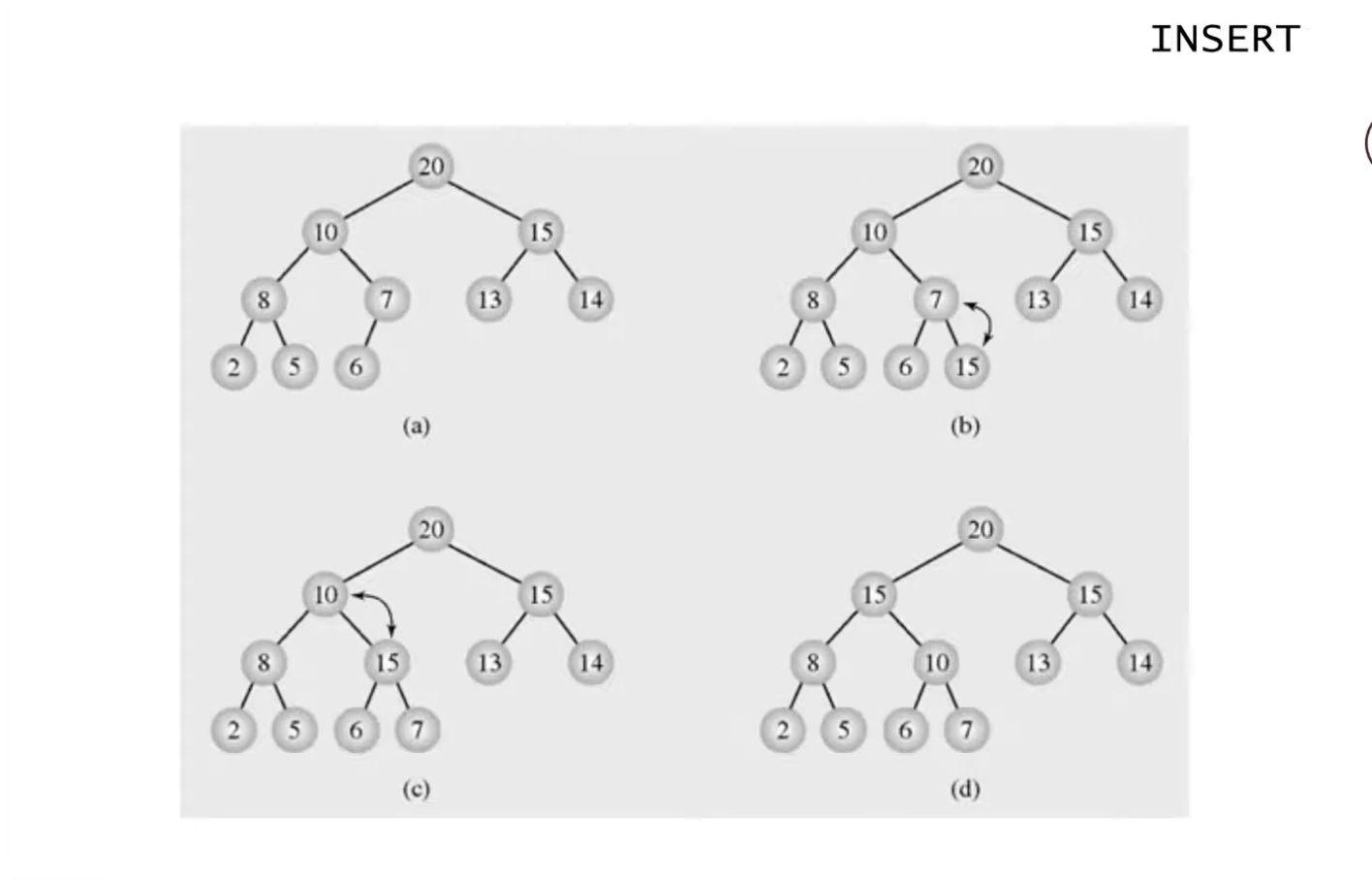
1. 새로운 원소를 삽입하는 과정은,
heap은 완전 이진 트리이기 때문에 새로운 값은 항상 제일 끝 노드로 추가되어야 한다.
이때 max heap property를 위반한다면 heap으로 바꿔주는 과정을 거쳐야 한다.
(max heap property : 부모 노드는 자식 노드보다 값이 크거나 같아야 함)
그림 (b)에서 새로운 값 15가 노드에 추가된다면, heap 조건을 만족시킬 때까지 부모 노드와 자리를 바꾼다.
계속해서 바꾸게 된다면 (d)와 같은 결과를 얻을 수 있고 heap 조건들을 만족하게 된다.
insert의 sudo code

A : 힙을 나타낸 1차원 배열
key : 추가되는 값
배열의 가장 마지막 위치인 heap_size에 추가하는 값을 넣고, (A[heap_size] = key)
가장 마지막 노드부터 (i = heap_size) 루트노드 전까지(i>1) 탐색하면서 부모노드가 추가한 값보다 작다면 부모 노드와 값을 바꿔주는 과정 (exchange A[i] and A[PARENT(i)]) 을 반복한다.
i 값을 현재 부모 노드 값과 바꿔주면서 ( i = PARENT(i) ) 루트노드 전까지 올라갈 수 있게 한다.
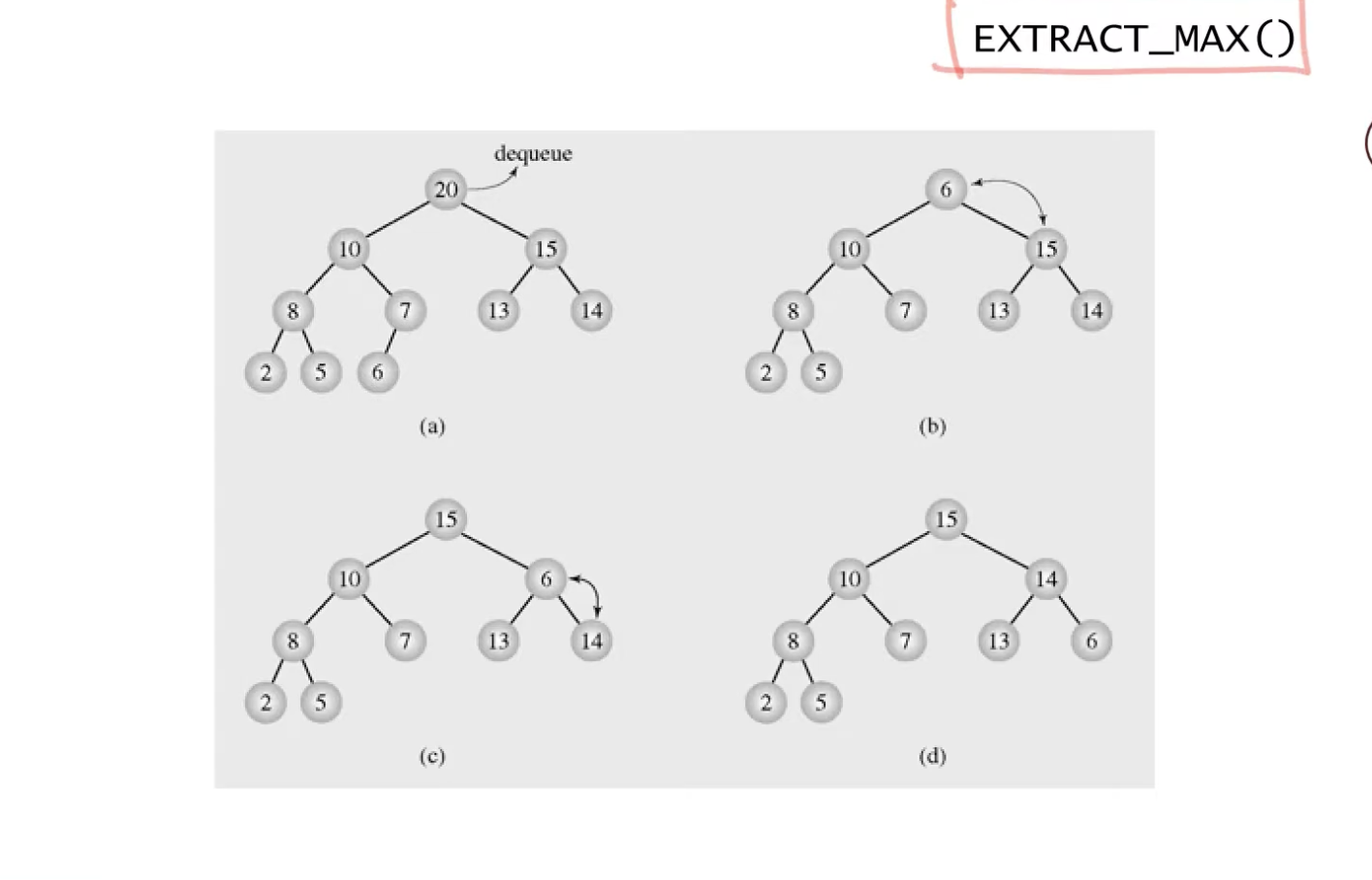
2. 최대값을 반환해주는 과정은,
max heap에서 루트 노드는 항상 최대값이 들어있기 때문에 루트 노드를 뽑아주면 최대값을 반환할 수 있다.
하지만 루트 노드의 값을 빼버리면 루트 노드가 비어 트리가 되지 않으니까
1) 트리의 가장 끝 노드를 루트 노드로 올려준다. 그림 (a) -> 그림 (b)
2) 그림 (b)는 max heap property를 만족하지 않으니 힙으로 만드는 heapify과정을 거쳐 힙으로 만들어준다.
( heapify : 자식 노드 중 더 큰 값과 위치를 바꿔주는 과정을 반복)
그림 (b)의 6은 자식 노드 중 더 큰 값인 15와 위치가 한 번 바뀌고, 아래 레벨에 내려와서는 자식 노드 중 더 큰 값인 14와 값이 바뀌어 max-heap이 된다.
extract_max의 sudo code

heap size가 1보다 작다면 (heap의 길이가 0) 에러를 띄워주거나 프로그램을 종료
루트 노드의 값을 max라는 변수에 담아 추출해주고 ( max <- A[1] )
비게되는 루트 노드를 트리의 마지막 노드 값으로 채워준다 ( A[1] <- A[heap_size[A]] )
heap_size[A]를 1 감소시켜 트리의 마지막 노드를 제거해줌으로써 다음 반복부터 트리의 길이가 -1 감소되게 만들어 준다.
여기까지 하게 된다면 그림 (b)까지 진행된 것이다.
여기서 MAX-HEAPIFY를 해주면서 그림 (b)였던 트리를 max heap으로 만들어 그림 (d)의 결과를 반환해준다.
이 과정을 반복해주면 최대값인 root 노드의 값을 차례대로 빼주면서 가장 높은 값부터 얻을 수 있다.
(값이 들어온 순서에 상관없이 '최대값 빼기 - heap 만들어 root에 최대값 올리기' 과정을 반복해 주니까)
이것은 최대 우선순위 큐라고 부르는 것이다.
'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 자바 알고리즘 문제풀이 #04-05 5. k번째 큰 수 (TreeSet) (0) | 2023.01.14 |
|---|---|
| [Inflearn] 자바 알고리즘 문제풀이 #04-04 4. 모든 아나그램 찾기(Hash, sliding window) (0) | 2023.01.13 |
| [Inflearn] 자바 알고리즘 문제풀이 #04-03 3. 매출액의 종류(Hash, sliding window) (0) | 2023.01.11 |
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - 힙 정렬 (heap sort) (0) | 2023.01.10 |
| [Inflearn] 자바 알고리즘 문제풀이 #04-02 2. 아나그램(해쉬) (0) | 2023.01.07 |



