Comparison sort VS Non-comparison sort

앞서 배웠던 버블정렬, 삽입정렬, 합병정렬, 퀵정렬, 힙정렬은 Comparision sort로 데이터들간의 크기만을 고려해서 정렬한다

하지만, 어떤 Comparison sort라도 최선의 경우 시간 복잡도가 O(n logn)보다 낮아질 수 없다.
왜냐하면 한 번의 sort를 돌 때 '최소' 트리의 높이만큼(log n) 탐색해야 하는데, 그 과정을 n번 반복하기 때문이다.
이러한 comparision sort의 한계점을 넘어서기 위해,
데이터들간의 크기 + 그 데이터들에 대한 사전지식 정보를 이용해 O(logn)의 시간복잡도(Sorting in Linear Time)를 갖는 정렬 알고리즘에 대해 알아보자.
1) Counting Sort

데이터의 크기 정보와 추가로 그 데이터들이 어떤 범위에 있는지의 사전지식 정보가 필요하다.
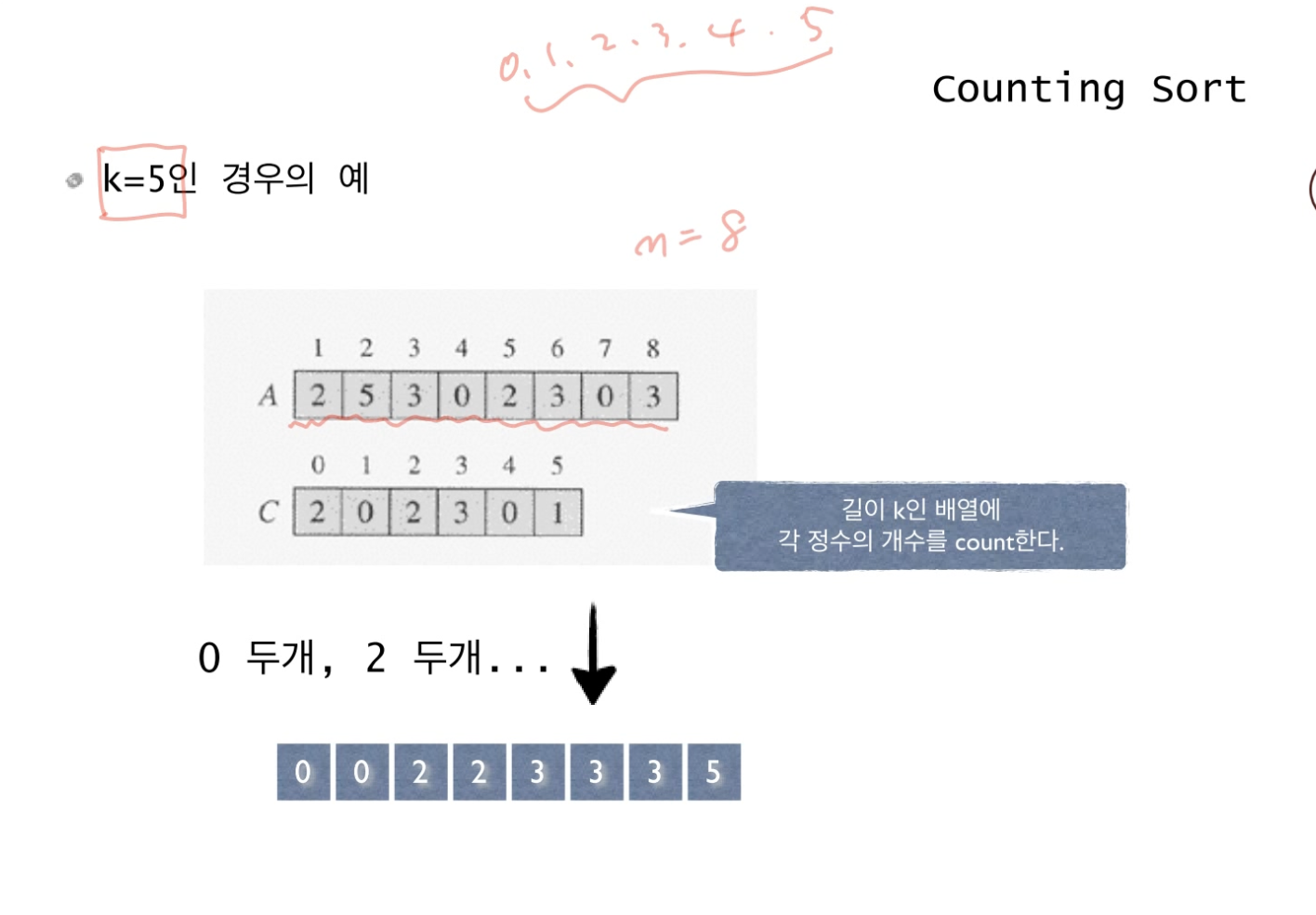
0~5 범위에 있는 8개의 숫자를 C배열에 세어준다면, 0은 2개, 1은 0개, ..., 5는 1개로 셀 수 있다.
C배열에 있는 값의 개수만큼 순서대로 꺼내주면 0, 0, 2, 2, 3, 3, 3, 5의 정렬된 결과를 가져올 수 있다.
Counting Sort의 sudo code

A배열 안에 있는 정렬할 데이터를 C배열에 해당 인덱스의 값으로 넣어주면서 해당 숫자의 개수를 센다.
C배열을 토대로 정렬된 결과를 다시 A배열에 넣어준다.
하지만 counting sort의 경우 같은 값을 가져도, 그 값들은 레코드의 일부분이기 때문에(같은 행에 다른 값들을 같이 가지고 움직이기 때문에) 앞서 나왔던 값이 정렬된 후에도 앞에 나오게 정렬하는 것이 중요하다.
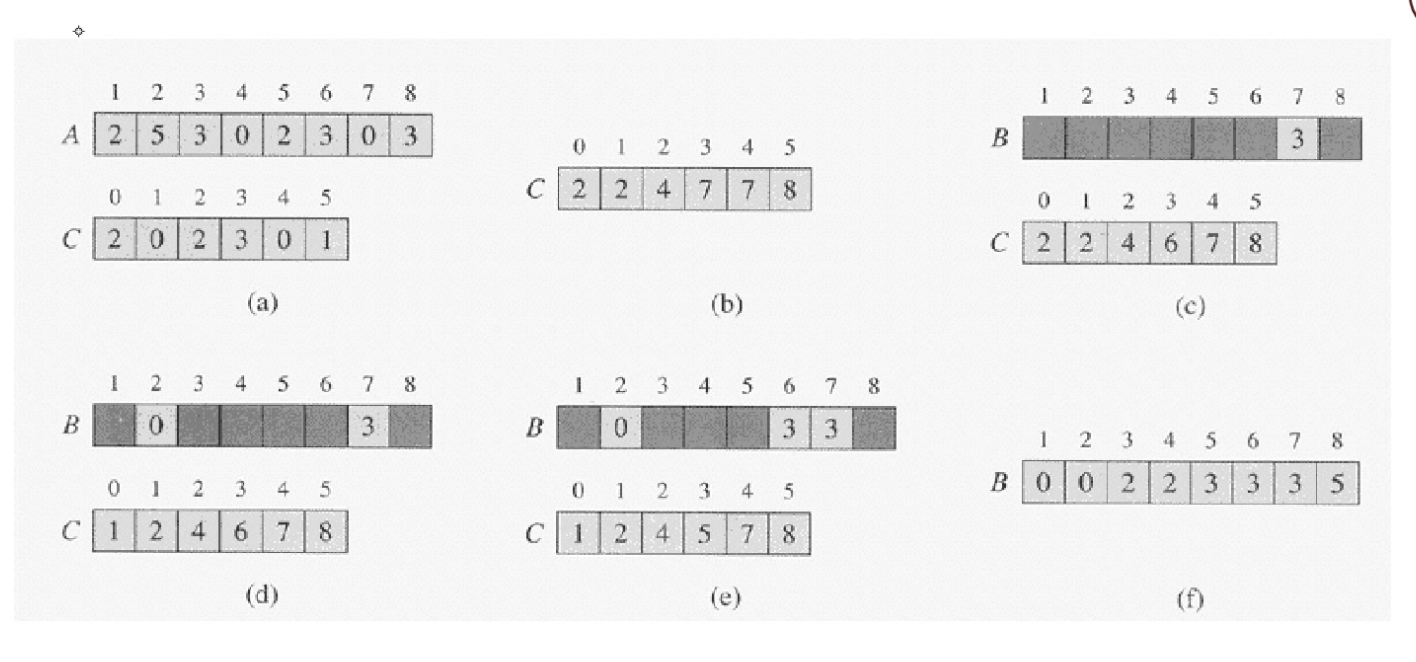
그렇게 만드는 방법은 그림(a)처럼 C배열에 숫자를 세어준 후, C배열의 누적합을 이용하면 된다.
누적합이 있는 배열을 사용하여 A배열의 끝 값부터 B배열에 정렬된 결과를 넣어준다.
방법은 그림(a)의 가장 끝 값인 3은 C배열의 인덱스 3에 들은 값을 위치로 가진다.
따라서 C배열의 인덱스 3에 들은 값은 7이기 때문에 B배열의 인덱스 7번에 넣어준 후 C배열에서 참조했던 값을 -1해주면 된다.
A배열의 끝 값부터 처음 값까지 해당 과정을 반복하면 그림(f)의 정렬된 결과를 얻을 수 있다.(레코드 순서도 보존한)
개선된 Counting Sort의 sudo code


Counting Sort의 시간복잡도는 O(n)으로 linear하다.
"입력에 동일한 값이 있을 때 입력에 먼저 나오는 값이 출력에서도 먼저 나오는" stable 정렬 알고리즘이다.
2. Radix Sort
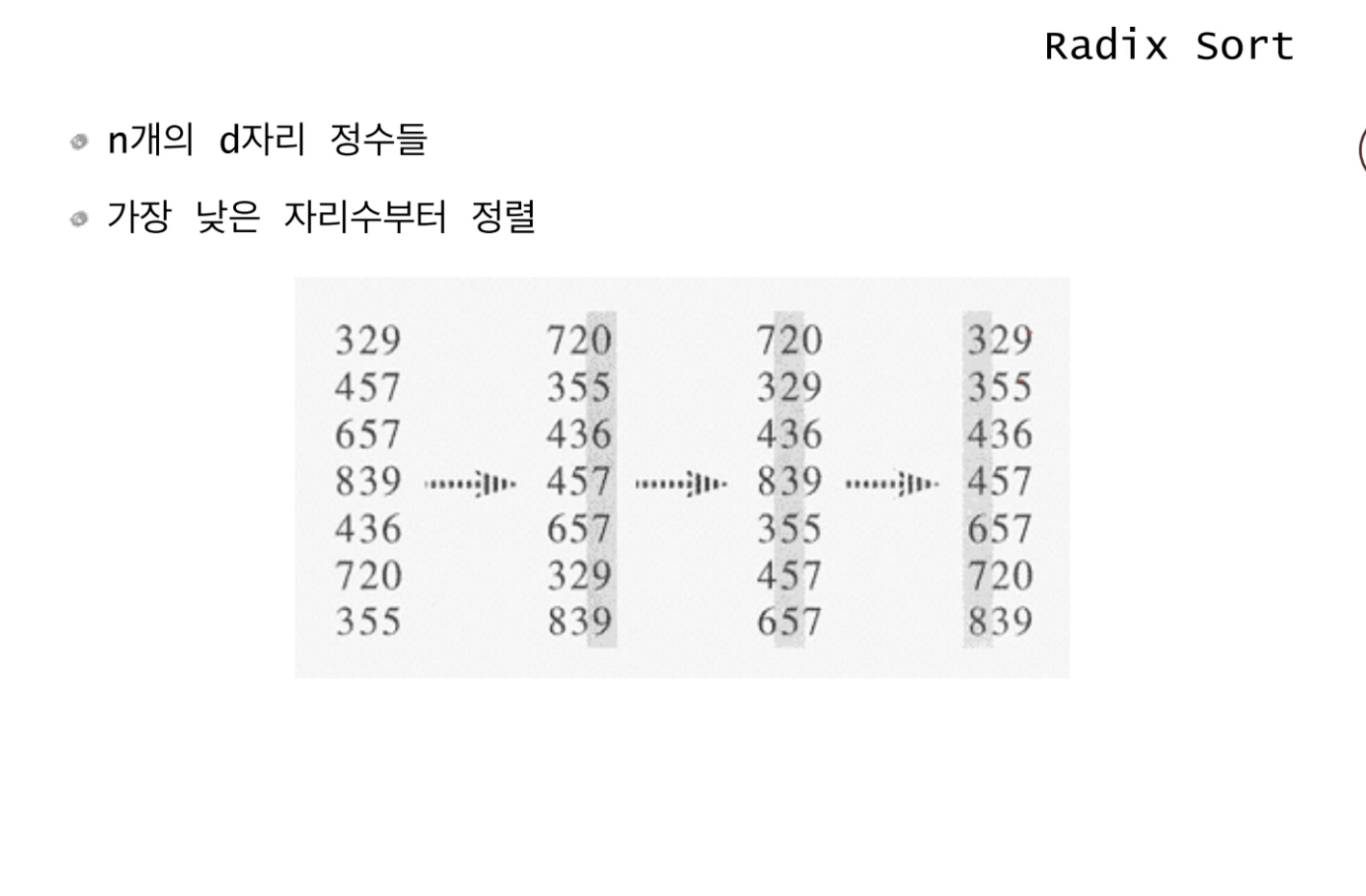
끝의 자리수부터 정렬하는 간단한 알고리즘이다.
데이터의 크기 정보와 추가로 그 데이터들이 몇 자리 수인지의 사전지식 정보가 필요하다.
Radix Sort의 sudo code

수도 코드는 굉장히 단순하다. 자리 수 만큼 반복하며 정렬해주면 된다.
d자리 정수라면 1의 자리 수, 2의 자리 수, ...., d의 자리 수까지 정렬을 반복한다.
시간 복잡도는 O(n)으로 linear하다.
'Algorithm > Inflearn' 카테고리의 다른 글
| [Inflearn] 자바 알고리즘 문제풀이 #05-04 4. 후위식 연산(postfix) (0) | 2023.01.21 |
|---|---|
| [Inflearn] 영리한 프로그래밍을 위한 알고리즘 - Sorting in Java (1) | 2023.01.17 |
| [Inflearn] 자바 알고리즘 문제풀이 #05-03 3. 크레인 인형뽑기(카카오) (0) | 2023.01.16 |
| [Inflearn] 자바 알고리즘 문제풀이 #05-02 2. 괄호문자제거 (0) | 2023.01.15 |
| [Inflearn] 자바 알고리즘 문제풀이 #05-01 1. 올바른 괄호 (0) | 2023.01.14 |



