다음 그래프에서 1번 정점에서 각 정점으로 가는 최소 이동 간선 수를 출력하세요.
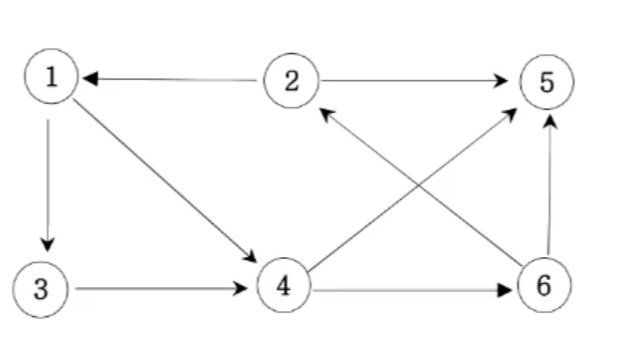
입력
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다.
그 다음부터 M줄에 걸쳐 연결정보가 주어진다.
출력
총 가지수를 출력한다.
예시 입력 1
6 9
1 3
1 4
2 1
2 5
3 4
4 5
4 6
6 2
6 5
예시 출력 1
2 : 3
3 : 1
4 : 1
5 : 2
6 : 2
코드
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class 그래프최단거리BFS {
static int n, m, answer=0;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch, dis;
public void BFS(int v){
Queue<Integer> Q = new LinkedList();
ch[1] = 1;
dis[1] = 0;
Q.offer(v);
while(!Q.isEmpty()) {
int cv = Q.poll();
for(int nv : graph.get(cv)) {
if(ch[nv]==0) {
ch[nv]=1;
Q.offer(nv);
dis[nv] = dis[cv]+1;
}
}
}
}
public static void main(String[] args) {
그래프최단거리BFS T = new 그래프최단거리BFS();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new ArrayList<ArrayList<Integer>>();
ch = new int[n+1];
dis = new int[n+1];
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<Integer>());
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b);
}
T.BFS(1);
for (int i = 2; i <= n; i++) {
System.out.println(i + " : " + dis[i]);
}
}
}
결과

1번 정점에서 2번 정점까지 가는 최소 이동 간선 수 : 3 ==> 1 - 4 - 6 - 2 (3개)
1번 정점에서 3번 정점까지 가는 최소 이동 간선 수 : 1 ==> 1 - 3 (1개)
1번 정점에서 4번 정점까지 가는 최소 이동 간선 수 : 1 ==> 2 - 4 (1개)
1번 정점에서 5번 정점까지 가는 최소 이동 간선 수 : 2 ==> 1 - 4 - 5 (2개)
1번 정점에서 6번 정점까지 가는 최소 이동 간선 수 : 2 ==> 1 - 4 - 6 (2개)
출처 : 인프런 자바 알고리즘 문제풀이 입문 : 코딩테스트 대비
'Language > JAVA' 카테고리의 다른 글
| [JAVA] 인터페이스 개념과 장점 쉬운 예시로 이해하기 (3) | 2023.12.21 |
|---|---|
| 자바 클래스와 객체 관계에서 스프링적 사고하기 (1) | 2023.12.17 |
| [JAVA] 자바 그래프 경로탐색 DFS 인접행렬, 인접리스트 (0) | 2023.03.27 |
| [JAVA] 자바 그래프와 인접행렬 (0) | 2023.03.26 |
| [JAVA] 자바 피보나치 재귀 (메모이제이션) (0) | 2023.03.20 |


